
���� ��1�������ܷ��õ����������Դ��ۺ�ĵ��ۣ���y��=60��0.8x��������������������ܷ��ã��������ۣ���0��x��20ʱ��y��=60��0.9x����x��20ʱ��y��=60��0.9��20+60��0.7��x-20����
��2����x=32�ֱ���루1���ж�Ӧ�ú�����ϵ����y����y����ֵ��Ȼ��Ƚϴ�С���ɣ�
��� �⣺��1����������������ܷ��ã�y��=60��0.8x=48x��
��������������ܷ��ã���0��x��20ʱ��y��=60��0.9x=54x����x��20ʱ��y���T60��0.9��20+60��0.7��x-20��=42x+240��
��2����x=32ʱ��y��=48��32=1536��Ԫ����y��=42��32+240=1584��
��Ϊy����y����
���Ժ���ʦѡ��������磮
���� ���⿼����һ�κ�����Ӧ�ã�����ʵ�������е�������ϵ����һ�κ�����ϵ���ر������������ܷ���Ҫ���÷ֶκ���������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
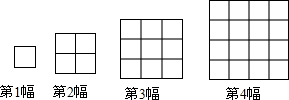 ��1�����2��ͼ��ʾ����2��2�ķ����й����������Σ�ͼ����2��2��
��1�����2��ͼ��ʾ����2��2�ķ����й����������Σ�ͼ����2��2�� ��1��1��
��1��1��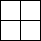 ����2��2+1��1=5��������
����2��2+1��1=5�������� ��2��2��
��2��2�� ��1��1��
��1��1��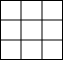 ����14��������
����14�������� ��3��3��
��3��3�� ��2��2��
��2��2�� ��1��1��
��1��1�� ����30��������
����30�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
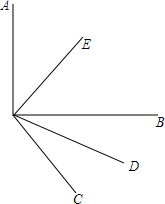 ��ͼ��ʾ����֪OEƽ�֡�AOB��ODƽ�֡�BOC����AOBΪֱ�ǣ���COD=20�㣬���EOC�Ķ�����
��ͼ��ʾ����֪OEƽ�֡�AOB��ODƽ�֡�BOC����AOBΪֱ�ǣ���COD=20�㣬���EOC�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
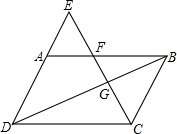 ��֪E��ƽ���ı���ABCD��DA���ӳ����ϵ�һ�㣬��$\frac{EA}{AD}=\frac{1}{2}$������EC���ֱ�AB��BE�ڵ�F��G������ADC=45�㣬ED=3$\sqrt{2}$��DC=6��
��֪E��ƽ���ı���ABCD��DA���ӳ����ϵ�һ�㣬��$\frac{EA}{AD}=\frac{1}{2}$������EC���ֱ�AB��BE�ڵ�F��G������ADC=45�㣬ED=3$\sqrt{2}$��DC=6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2+2xy+y2=0 | B�� | x��x+3��=x2-1 | C�� | ��x-1����x-3��=0 | D�� | $x+\frac{1}{x}=0$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com