
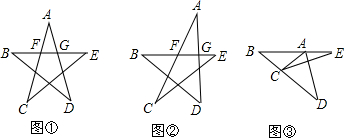
���� �����Ķ����ϡ��������ڽǺͶ����������ε���ǵ����ʡ����ͼ�ν�ü��ɣ�
��� �⣺̽�����ߡ�AFG=��C+��E����AGF=��B+��D��
���AFG+��AGF=��C+��E+��B+��D��
�ߡ�A+��AFG+��AGF=180�㣬
���A+��B+��C+��D+��E=180�㣬
���A=��B=��C=��D=��E=36�㣻
��չ���ߡ�AFG=��C+��E����AGF=��B+��D��
���AFG+��AGF=��C+��E+��B+��D��
�ߡ�A+��AFG+��AGF=180�㣬
���A+��B+��C+��D+��E=180�㣻
Ӧ�ã���CAD+��ACE+��E=180��-��EAD=180��-��B-��D=108�㣮
���� ���⿼������������ڽǺͶ�������������ǵ����ʣ������������ڽǺ͵���180��������ε�һ����ǵ��ں��������ڵ������ڽǵĺ��ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
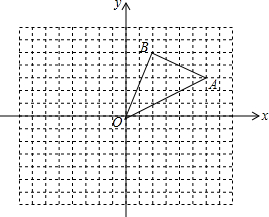 ��ͼ���ڱ߳�Ϊ1����������ɵ������У���AOB�Ķ�����ڸ���ϣ���A��B������ֱ�Ϊ��6��3������2��5��
��ͼ���ڱ߳�Ϊ1����������ɵ������У���AOB�Ķ�����ڸ���ϣ���A��B������ֱ�Ϊ��6��3������2��5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{27}=3\sqrt{3}$ | B�� | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C�� | $\sqrt{5}��\sqrt{3}=\sqrt{15}$ | D�� | $\sqrt{8}��\sqrt{2}=2$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ѧϰ�������ε����֪ʶ����ʦ��С÷���˵���ҵ�⣬�����С÷��������⣮
��ѧϰ�������ε����֪ʶ����ʦ��С÷���˵���ҵ�⣬�����С÷��������⣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com