
【题目】如图,是同-种蔬菜的两种裁植方法.甲:![]() 四珠顺次连结成为一个菱形,且
四珠顺次连结成为一个菱形,且![]() .乙:
.乙:![]() 四株连结成一个正方形。其中两行作物间的距离为行距;一行中相邻两株作物的距离为株距:设这两种蔬菜充分生长后,每株在地面上的影子近似成一个圆面(相邻两圆如图相切),其中阴影部分的面积表示生长后空隙地面积。设株距都为
四株连结成一个正方形。其中两行作物间的距离为行距;一行中相邻两株作物的距离为株距:设这两种蔬菜充分生长后,每株在地面上的影子近似成一个圆面(相邻两圆如图相切),其中阴影部分的面积表示生长后空隙地面积。设株距都为![]() ,其它客观因素都相同.则对于下列说法:
,其它客观因素都相同.则对于下列说法:
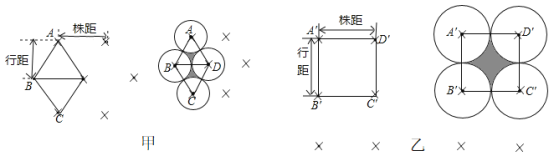
①甲的行距比乙的小;②甲的行距为![]() ;③甲、乙两种栽植方式,蔬菜形成的影子面积相同;④甲的空隙地面积比乙的空隙地面积少
;③甲、乙两种栽植方式,蔬菜形成的影子面积相同;④甲的空隙地面积比乙的空隙地面积少![]() .其中正确的个数为( )
.其中正确的个数为( )
A.1B.2C.3D.4
科目:初中数学 来源: 题型:
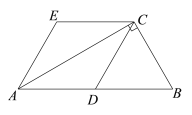
【题目】已知:如图,楼顶有一根天线,为了测量楼的高度,在地面上取成一条直线的三点E、D、C,在点C处测得天线顶端A的仰角为60°,从点C走到点D,CD=6米,从点D处测得天线下端B的仰角为45°.又知A、B、E在一条线上,AB=25米,求楼高BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90,D为AB的中点,AE∥DC,CE∥DA.
(1)求证:四边形ADCE是菱形;
(2)连接DE,若AC =![]() ,BC =2,求证:△ADE是等边三角形.
,BC =2,求证:△ADE是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是该型号电风扇近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
![]() 求A、B两种型号的电风扇的销售单价;
求A、B两种型号的电风扇的销售单价;
![]() 若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年疫情期间,为防止疫惰扩散,人们见面的机会少了,但是随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.为此,李老师设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),进行调查.将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次参与调查的共有_______人:在扇形统计图中,表示“微信”的扇形圆心角的度数为_______;其它沟通方式所占的百分比为_______;
(2)将条形统计图补充完整;
(3)如果我国有13亿人在使用手机.①请估计最喜欢用“微信”进行沟通的人数:并:用科学计数法表示;②在全国使用手机的人中随机抽取一人,用频率估计概率,求抽取的恰好使用“QQ”的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
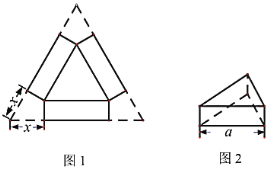
【题目】如图1,小明用一张边长为![]() 的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为
的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为![]() ,再折成如图2所示的无盖糖果盒,它的容积记为
,再折成如图2所示的无盖糖果盒,它的容积记为![]() .
.
(1)![]() 关于
关于![]() 的函数关系式是__________,自变量
的函数关系式是__________,自变量![]() 的取值范围是__________.
的取值范围是__________.
(2)为探究![]() 随
随![]() 的变化规律,小明类比二次函数进行了如下探究:
的变化规律,小明类比二次函数进行了如下探究:
①列表:请你补充表格中的数据:
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| 0 | 3.125 | ________ | 3.375 | ________ | 0.625 | 0 |
②描点:请你把上表中各组对应值作为点的坐标,在平面直角坐标系中描出相应的点;
③连线:请你用光滑的曲线顺次连接各点.

(3)利用函数图象解决:
①该糖果盒的最大容积是__________;
②若该糖果盒的容积超过![]() ,请估计糖果盒的底边长
,请估计糖果盒的底边长![]() 的取值范围.(保留一位小数)
的取值范围.(保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC .
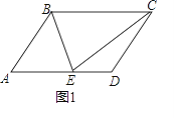
(1)如图1,判断△BCE的形状,并说明理由;
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com