
 如图,将长方形ABCD沿BD对折,C点落在C′的位置,BC′与AD交于点E.
如图,将长方形ABCD沿BD对折,C点落在C′的位置,BC′与AD交于点E. 解:(1)由题意得:∠EBD=∠CBD;
解:(1)由题意得:∠EBD=∠CBD;

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、①②③ | B、①③④ |
| C、③④ | D、①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,BE、CF是△ABC的两条高,它们相交于点Q,CQ=AB,连结AQ,延长BE到P,使BP=AC.
如图,BE、CF是△ABC的两条高,它们相交于点Q,CQ=AB,连结AQ,延长BE到P,使BP=AC.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC=
已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC=| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
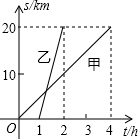 甲、乙二人沿着相同的路线由A地到B地匀速行进.已知A、B两地间的路程为20km,他们行进的路程s(km)与行进的时间t(h)之间的函数关系如图所示.根据图象信息,下列说法不正确的是( )
甲、乙二人沿着相同的路线由A地到B地匀速行进.已知A、B两地间的路程为20km,他们行进的路程s(km)与行进的时间t(h)之间的函数关系如图所示.根据图象信息,下列说法不正确的是( )| A、甲的速度是5km/h |
| B、乙的速度是20km/h |
| C、乙比甲晚出发1h |
| D、甲走完全程比乙走完全程多用了2h |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com