练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．下列各式计算正确的是（　　）
    A．a+3a2=3a3B．（a-b）2=a2-ab+b2C．2（a-b）=2a-2bD．（2ab）2÷ab=2ab

    分析 各项计算得到结果，即可作出判断．

    解答 解：A、原式不能合并，不符合题意；
    B、原式=a2-2ab+b2，不符合题意；
    C、原式=2a-2b，符合题意；
    D、原式=4a2b2÷ab=4ab，不符合题意，
    故选C

    点评 此题考查了整式的混合运算，熟练掌握公式及法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    12．如图1～3，在直角边分别为3和4的直角三角形中，每多作一条斜边上的高就增加一个三角形的内切圆，依此类推，图6中有6个直角三角形的内切圆，它们的面积分别记为S1，S2，S3，…，S6，则S1+S2+S3+…+S6的值是（　　）
    A．πB．$\sqrt{2}$πC．1.6πD．$\frac{3}{2}$π

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．体育老师统计了某一小组8个人的数学成绩，成绩如下（单位为分）：55，56，56，57，58，55，56，56，这组数据的众数是（　　）
    A．55B．56C．57D．58

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列运算正确的是（　　）
    A．（a+b）2=a2+b2B．（3a2）3=9a6C．50÷5-2=$\frac{1}{25}$D．$\sqrt{8}$-$\sqrt{50}$=-3$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

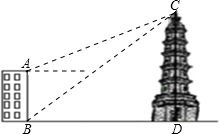    17．如图，大楼AB高16m，远处有一塔CD，某人在楼底B处测得塔顶C的仰角为39°，在楼顶A处测得塔顶的仰角为22°，求塔高CD的高．（结果保留小数后一位）
    参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40，si39°≈0.63，cos39°≈0.78，tan39°≈0.81．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．（1）计算：|1-$\sqrt{3}$|-$\sqrt{12}$+2cos30°-20170；
    （2）解不等式组$\left\{\begin{array}{l}2-x≤3\\ \frac{3}{2}x+1＞x-\frac{3}{2}.\end{array}\right.$并求其最小整数解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．一次数学测试，某小组五名同学的成绩如下表（有两个数据被遮盖）：
    组员甲乙丙丁戊方差/分2平均成绩/分
    成绩/分8179■8082■80
    那么被遮盖的两个数据依次是（　　）
    A．80、2B．80、10C．78、2D．78、10

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．对任意一个三位数n，如果n满足各数位上的数字互不相同，且都不为零，那么称这个数为“相异数”．将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为F（n）．例如n=123，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和为213+321+132=666，666÷111=6，所以F（123）=6．
    （1）计算：F（243），F（617）；
    （2）若s，t都是“相异数”，其中s=100x+32，t=150+y（1≤x≤9，1≤y≤9，x，y都是正整数），规定：k=$\frac{F（s）}{F（t）}$，当F（s）+F（t）=18时，求k的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．若a2=（-5）2，b3=（-5）3，则a+b的值是0或-10．

    查看答案和解析>>

    同步练习册答案