
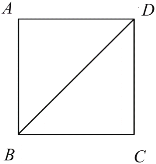
【题目】如图,正方形![]() 中,
中,![]() ,点
,点![]() 是正方形所在平面内一动点,满足
是正方形所在平面内一动点,满足![]() .
.
(1)当点![]() 在直线
在直线![]() 上方且
上方且![]() 时,求证:
时,求证:![]() ;
;
(2)若![]() ,求点
,求点![]() 到直线
到直线![]() 的距离;
的距离;
(3)记![]() ,在点
,在点![]() 运动过程中,
运动过程中,![]() 是否存在最大值或最小值?若存在,求出其值,若不存在,说明理由.
是否存在最大值或最小值?若存在,求出其值,若不存在,说明理由.
【答案】(1)见解析;(2)![]() 或
或![]() ;(3)当
;(3)当![]() 时,
时,![]() 最小值为
最小值为![]() .当点
.当点![]() 在直线
在直线![]() 下方时,
下方时,![]() 有最大值
有最大值![]()
【解析】
(1)利用勾股定理的逆定理证明△ADQ是等腰直角三角形即可解决问题.
(2)如图2中,由题意点Q是以D为圆心,DQ为半径的圆和以BD为直径的圆的交点(有两种情形,图中Q,Q′).连接BQ,BQ′,过点A作AH⊥BQ于H,过点A作AH′⊥BQ′于H,AH′交BQ于J.解直角三角形求出AH,BH即可解决问题.
(3)如图3-1中,当AQ<BQ时,过点A作QJ⊥AB交BA的延长线于J.AQ2-BQ2=JQ2+AJ2-(JQ2+BJ2)=AJ2-BJ2=(AJ+BJ)(JA-BJ)=-AB(2JA+AB)=![]() (2JA+
(2JA+![]() ),观察图象可知,当JA的值最大时,AQ2-BQ2的值最小,此时点Q在CD的延长线上.如图3-2中,当QA>QB时,过点A作QJ⊥AB交BA的延长线于J.AQ2-BQ2=JQ2+AJ2-(JQ2+BJ2)=AJ2-BJ2=(AJ+BJ)(JA-BJ)=AB(AJ-BJ),观察图象可知,当JA-JB的值最大时,AQ2-BQ2的值最大,此时点Q在线段CD上.
),观察图象可知,当JA的值最大时,AQ2-BQ2的值最小,此时点Q在CD的延长线上.如图3-2中,当QA>QB时,过点A作QJ⊥AB交BA的延长线于J.AQ2-BQ2=JQ2+AJ2-(JQ2+BJ2)=AJ2-BJ2=(AJ+BJ)(JA-BJ)=AB(AJ-BJ),观察图象可知,当JA-JB的值最大时,AQ2-BQ2的值最大,此时点Q在线段CD上.
解:(1)证明:如图1中,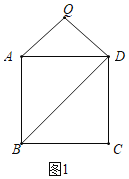
∵AQ=DQ=1,AD=![]() ,
,
∴AQ2+DQ2=AD2,
∴∠Q=90°,
∴∠QAD=∠ADQ=45°,
∵四边形ABCD是正方形,
∴∠ADB=45°,
∴∠ADB=∠QAD,
∴AQ∥BD.
(2)解:如图2中,由题意点Q是以D为圆心,DQ为半径的圆和以BD为直径的圆的交点(有两种情形,图中Q,Q′).
连接BQ,BQ′,过点A作AH⊥BQ于H,过点A作AH′⊥BQ′于H,AH′交BQ于J.
∵BD=![]() AD=2,QD=1,
AD=2,QD=1,
∴BQ=2DQ,
∴∠QBD=30°,同法可得∠DBQ′=30°,
∵四边形ABCD是正方形,
∴∠ABD=∠CBD=45°,
∴∠ABQ=∠CBQ′=15°,
∴∠ABH′=75°,∠BAJ=15°,
∴∠JAB=∠JBA=15°,
∴∠AJH=∠JAB+∠JBA=30°,
设AH=a,则AJ=JB=2AH=2a,JH=![]() ,
,
在Rt△ABH中,则有2=a2+(2a+![]() )2,
)2,
解得a=![]() ,
,
∴AH=![]() ,BH=
,BH=![]() ,
,
∵∠AHB=∠AH′B=90°,∠ABH=∠BAH′,AB=BA,
∴△AHB≌△BH′A(AAS),
∴AH′=BH=![]() ,
,
∴点A到直线BQ的距离为![]() 或
或![]() .
.
(3)解:如图3-1中,当AQ<BQ时,过点A作QJ⊥AB交BA的延长线于J.
∵AQ2-BQ2=JQ2+AJ2-(JQ2+BJ2)=AJ2-BJ2=(AJ+BJ)(JA-BJ)=-AB(2JA+AB)=![]() (2JA+
(2JA+![]() ),
),
观察图象可知,当JA的值最大时,AQ2-BQ2的值最小,此时点Q在CD的延长线上,
最小值=![]() (2+
(2+![]() )=
)=![]() .
.
如图3-2中,当QA>QB时,过点A作QJ⊥AB交BA的延长线于J.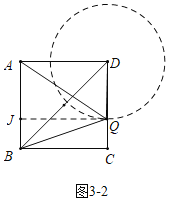
∵AQ2-BQ2=JQ2+AJ2-(JQ2+BJ2)=AJ2-BJ2=(AJ+BJ)(JA-BJ)=AB(AJ-BJ),
观察图象可知,当JA-JB的值最大时,AQ2-BQ2的值最大,此时点Q在线段CD上,
最大值=![]() (1-
(1-![]() +1)=2
+1)=2![]() -2.
-2.


科目:初中数学 来源: 题型:
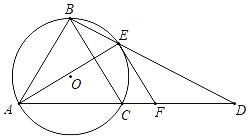
【题目】如图,⊙O是△ABC的外接圆,AB=BC,延长AC到点D,使得CD=CB,连接BD交⊙O于点E,过点E做BC的平行线交CD于点F.
(1)求证:AE=DE.
(2)求证:EF为⊙O的切线;
(3)若AB=5,BE=3,求弦AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 在
在![]() 的边上按
的边上按![]() 的路线匀速移动,当点
的路线匀速移动,当点![]() 到达
到达![]() 点时停止移动;动点
点时停止移动;动点![]() 以
以![]() 的速度在
的速度在![]() 的边上按
的边上按![]() 的路线匀速移动,当点
的路线匀速移动,当点![]() 到达
到达![]() 点时停止移动.已知点
点时停止移动.已知点![]() 、点
、点![]() 同时开始移动,同时停止移动(即同时到达各自的终止位置).设动点
同时开始移动,同时停止移动(即同时到达各自的终止位置).设动点![]() 移动的时间为
移动的时间为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 与
与![]() 的函数关系如图②所示.
的函数关系如图②所示.
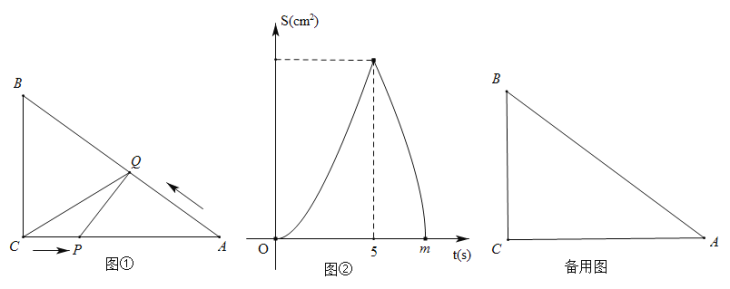
(1)图①中![]()
![]() ,图②中
,图②中![]()
![]() ;
;
(2)求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
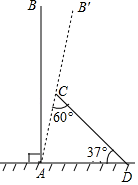
【题目】某次台风来袭时,一棵笔直大树树干AB(假定树干AB垂直于水平地面)被刮倾斜7°(即∠BAB′=7°)后折断倒在地上,树的顶部恰好接触到地面D处,测得∠CDA=37°,AD=5米,求这棵大树AB的高度.(结果保留根号)(参考数据:sin37≈0.6,cos37=0.8,tan37≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 上的点,且
上的点,且![]() ,连接
,连接![]() 、
、![]() 交于点
交于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中正确的结论个数是( )
;其中正确的结论个数是( )
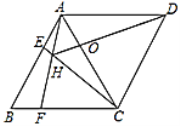
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源,生活垃圾一般按如图所示A、B、C、D四种分类方法回收处理,某城市环保部门为了提高宣传实效,抽样调查、统计了部分居民小区一段时间内生活垃圾的分类处理情况,并将调查统计结果绘制成如下两幅不完整的统计图表:
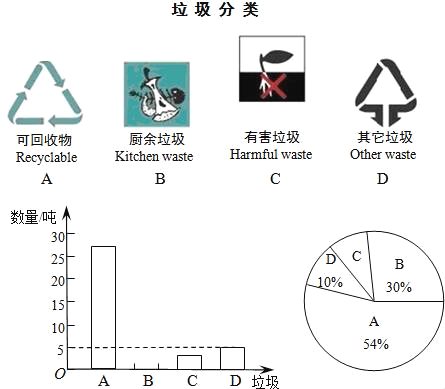
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共 吨;
(3)调查发现,在可回收物中塑料类垃圾占![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.
(k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张正面分别写有数字:﹣3,﹣2,0,1,2的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀.
(1)从中任意抽取一张卡片,则所抽卡片上数字的绝对值不小于1的概率是 ;
(2)先从中任意抽取一张卡片,以其正面数字作为m的值,然后再从剩余的卡片中随机抽一张,以其正面的数字作为n的值,请用列表法或画树状图法,求点Q(m,n)在第四象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com