
| A. | $\left\{\begin{array}{l}{\frac{x}{15}-15=y}\\{\frac{x}{12}+12=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{x}{15}+15=y}\\{\frac{x}{12}-12=y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{15}-\frac{24}{60}=y}\\{\frac{x}{12}-\frac{15}{60}=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{15}+\frac{24}{60}=y}\\{\frac{x}{12}-\frac{15}{60}=y}\end{array}\right.$ |
分析 设通讯员到达某地的路程是x千米,原定的时间为y小时,根据通讯员要在规定时间内到达某地,他每小时走15千米,则可提前24分钟到达某地;如果每小时走12千米,则要迟到15分钟列出方程组.
解答 解:设通讯员到达某地的路程是x千米,原定的时间为y小时,由题意得:
$\left\{\begin{array}{l}{\frac{x}{15}+\frac{24}{60}=y}\\{\frac{x}{12}-\frac{15}{60}=y}\end{array}\right.$,
故选D.
点评 此题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系,列出方程组.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
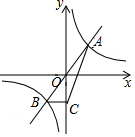 如图,已知函数y=kx 与函数y=$\frac{k}{x}$的图象交于A、B 两点,过点B作BC⊥y 轴,垂足为C,连接AC.若△ABC 的面积为2,则k 的值为2.
如图,已知函数y=kx 与函数y=$\frac{k}{x}$的图象交于A、B 两点,过点B作BC⊥y 轴,垂足为C,连接AC.若△ABC 的面积为2,则k 的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
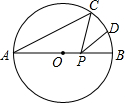 如图,在半径为1的⊙O中,∠BAC=30°,点D是劣弧CB的中点,点P是直径AB上的一个动点,则CP+DP的最小值为( )
如图,在半径为1的⊙O中,∠BAC=30°,点D是劣弧CB的中点,点P是直径AB上的一个动点,则CP+DP的最小值为( )| A. | $\sqrt{2}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
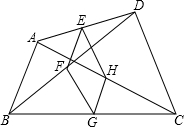 如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )
如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )| A. | AB∥DC | B. | AC=BD | C. | AC⊥BD | D. | AB=DC |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
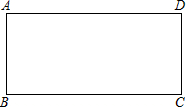 如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的情况下,请补充一个条件,使四边形ABCD成为矩形,这个条件是∠A=90°.
如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的情况下,请补充一个条件,使四边形ABCD成为矩形,这个条件是∠A=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com