Question

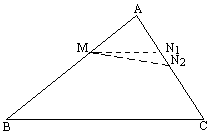
如图所示，已知△ABC中，AB＝9，AC＝6，点M在AB上，且AM＝3，点N在AC上，连接MN，如果△AMN与原三角形相似，那么AN的值为多少？

Answer 1

答案：
解析：

解答：(1)当△AMN∽△ACB时，＝　　又AB＝9，AC＝6，AM＝3，所以AN的值为×9＝． 　　(2)△AMN∽△ABC时，＝，可求得AN＝·AC＝×6＝2．所以AN的值为2或． 　　分析：由于已知中的相似三角形没有给出对应顶点，只知道其中的公共顶点A，故应分两种情况讨论：(1)△AMN∽△ABC；(2)△AMN∽△ACB，其中第一种情况是平行相似，第二种情况是交叉相似，然后得到比例式，AN即可求．

提示：

注意：过三角形一边上的一点作与原三角形相似的三角形时，情况不唯一．给出顶点时是两种情况，若不给顶点则会出现四种情况．如图所示．△AMN、、△BND、均与原△ABC相似．