
分析 (1)根据勾股定理求出AD的长;
(2)作EH⊥AB于H,求出AE的长,根据正弦的概念求出点E到车架AB的距离.
解答 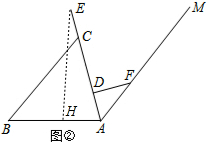 解:(1)在Rt△ADF中,由勾股定理得,
解:(1)在Rt△ADF中,由勾股定理得,
AD=$\sqrt{A{F}^{2}-F{D}^{2}}$=$\sqrt{252-202}$=15(cm;
(2)AE=AD+CD+EC=15+30+15=60(cm),
如图②,过点E作EH⊥AB于H,
在Rt△AEH中,sin∠EAH=$\frac{EH}{AE}$,
则EH=AE•sin∠EAH=AB•sin75°≈60×0.97=58.2(cm).
答:点E到AB的距离为58.2 cm.
点评 本题考查的是解直角三角形的知识,正确找出辅助线、掌握锐角三角函数的概念是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | x2+5x-1=x(x+5)-1 | B. | x2-4+3x=(x+2)(x-2)+3x | ||
| C. | x2-x+$\frac{1}{4}$=(x-$\frac{1}{2}$)2 | D. | 4x2-y2=(4x+y)(4x-y) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{361}{x-145}$-$\frac{361}{x}$=1.4 | B. | $\frac{361}{x}$-$\frac{361}{x-145}$=1.4 | ||
| C. | $\frac{361}{x}$-$\frac{361}{x+145}$=1.4 | D. | x+1.4(x+145)=361 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com