
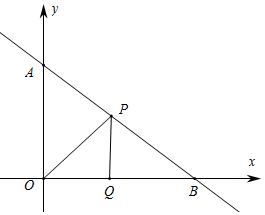
ЗжЮі ЃЈ1ЃЉШчЭМ1жаЃЌТњзуЬѕМўЕФЕуQгаШ§ИіЃЌЗжШ§жжЧщаЮЬжТлМДПЩЂйQO=QPЃЌЂкOP=OQЃЌЂлPO=PQЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌТњзуЬѕМўЕФЕуQга2ИіЃЎзїPQ1ЁЭOBгкQ1ЃЌQ2PЁЭOPгкQ2ЃЌПЩвджЄУїQ1ЁЂQ2ТњзуЬѕМўЃЌРэгЩЯрЫЦШ§НЧаЮЕФаджЪМДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉДцдкЃЎвдOQЮЊжБОЖзїЁбGЃЌЕБЁбGгыABЯрЧагкЕуPЪБЃЌЁЯOPQ=90ЁуЃЌДЫЪБOQЕФжЕзюаЁЃЎгЩДЫЧѓГіOQЃЌМДПЩНтОіЮЪЬтЃЎ
НтД№ НтЃКЃЈ1ЃЉШчЭМ1жаЃЌТњзуЬѕМўЕФЕуQгаШ§ИіЃЎ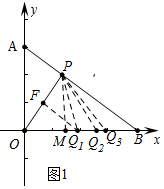
РэгЩЃКзїPMЁЭOBгкMЃЌзїOPЕФДЙжБЦНЗжЯпНЛOPгкFЃЌНЛOBгкQ1ЃЎдђQ1P=Q1OЃЌЁїOPQ1ЪЧЕШбќШ§НЧаЮЃЌДЫЪБOQ1=$\frac{1}{2}$OB=2ЃЎ
ЁпAЃЈ0ЃЌ3ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌ
ЁрOA=3ЃЌOB=4ЃЌAB=5ЃЌ
ЁпOPЁЭABЃЌ
Ёр$\frac{1}{2}$•OA•OB=$\frac{1}{2}$•AB•OPЃЌ
ЁрOP=$\frac{3ЁС4}{5}$=$\frac{12}{5}$ЃЌ
ЕБOQ2=OPЪБЃЌЁїOPQ2ЪЧЕШбќШ§НЧаЮЃЌДЫЪБOQ2=$\frac{12}{5}$ЃЌ
ЕБPO=PQ3ЪБЃЌЁпPMЁЭOQ3ЃЌ
ЁрOQ3=2OMЃЌ
ЁпЁЯPOM=ЁЯPOQ3ЃЌЁЯPMO=ЁЯOPBЃЌ
ЁрЁїOPMЁзЁїOBPЃЌ
ЁрOP2=OM•OBЃЌ
ЁрOM=$\frac{O{P}^{2}}{OB}$=$\frac{36}{25}$ЃЌ
ЁрOQ3=$\frac{72}{25}$ЃЎ
злЩЯЫљЪіЃЌЁїOPQЮЊЕШбќШ§НЧаЮЪБЃЌТњзуЬѕМўЕФЕуQгаШ§ИіЃЌOQЕФГЄЮЊ2Лђ$\frac{12}{5}$Лђ$\frac{72}{25}$ЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌТњзуЬѕМўЕФЕуQга2ИіЃЎ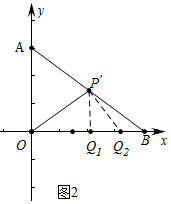
РэгЩЃКзїPQ1ЁЭOBгкQ1ЃЌQ2PЁЭOPгкQ2ЃЌ
ЁпPA=PBЃЌЁЯAOB=90ЁуЃЌ
ЁрPA=PB=POЃЌ
ЁрЁЯPOQ1=ЁЯABOЃЌЁпЁЯPQ1O=ЁЯAOBЃЌ
ЁрЁїOPQ1ЁзЁїBAOЃЌ
ЁпPA=PBЃЌPQ1ЁЮOAЃЌ
ЁрOQ1=BQ1=$\frac{1}{2}$OB=2ЃЌ
ЁпЁЯPOQ2=ЁЯABOЃЌЁЯOPQ2=ЁЯAOBЃЌ
ЁрЁїOPQ2ЁзЁїBOAЃЌ
Ёр$\frac{O{Q}_{2}}{AB}$=$\frac{OP}{OB}$ЃЌ
Ёр$\frac{O{Q}_{2}}{5}$=$\frac{\frac{5}{2}}{4}$ЃЌ
ЁрOQ2=$\frac{25}{8}$ЃЌ
злЩЯЫљЪіЃЌЁїOPQгыЁїABOЯрЫЦЪБЃЌТњзуЬѕМўЕФЕуQга2ИіЃЌOQЕФГЄЮЊ2Лђ$\frac{25}{8}$ЃЎ
ЃЈ3ЃЉДцдкЃЎРэгЩШчЯТЃК
ШчЭМ3жаЃЌвдOQЮЊжБОЖзїЁбGЃЌЕБЁбGгыABЯрЧагкЕуPЪБЃЌЁЯOPQ=90ЁуЃЌДЫЪБOQЕФжЕзюаЁЃЎ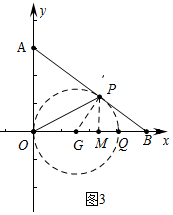
ЁрЩшOG=GP=rЃЌ
ЁпAO=AP=3ЃЌ
ЁрPB=AB=AP=2ЃЌ
дкRtЁїPBGжаЃЌЁпЁЯGPB=90ЁуЃЌPG=rЃЌBG=4-rЃЌPB=2ЃЌ
Ёрr2+22=ЃЈ4-rЃЉ2ЃЌ
Ёрr=$\frac{3}{2}$ЃЌ
ЁрOQ=2r=3ЃЌ
ЁрЕБ3ЁмOQЃМ4ЪБЃЌЁїOPQПЩЮЊжБНЧШ§НЧаЮЃЎ
зїPMЁЭOBгкMЃЎ
ЁпPMЁЮOAЃЌ
Ёр$\frac{PM}{OA}$=$\frac{PB}{AB}$=$\frac{BM}{BO}$ЃЌ
Ёр$\frac{PM}{3}$=$\frac{2}{5}$=$\frac{BM}{4}$ЃЌ
ЁрPM=$\frac{6}{5}$ЃЌBM=$\frac{8}{5}$ЃЌ
ЁрOM=4-$\frac{8}{5}$=$\frac{12}{5}$ЃЌ
ЁрOQШЁзюаЁжЕЪБЕуPЕФзјБъЃЈ$\frac{12}{5}$ЃЌ$\frac{6}{5}$ЃЉЃЎ
ЕуЦР БОЬтПМВщвЛДЮКЏЪ§злКЯЬтЁЂдВЕФгаЙиаджЪЁЂЧаЯпГЄЖЈРэЁЂЧаЯпЕФаджЪЁЂЯрЫЦШ§НЧаЮЕФХаЖЈКЭаджЪЁЂЙДЙЩЖЈРэЕШжЊЪЖЃЌНтЬтЕФЙиМќЪЧСщЛюдЫгУЫљбЇжЊЪЖНтОіЮЪЬтЃЌбЇЛсЬэМгГЃгУИЈжњЯпЃЌбЇЛсРћгУдВЕФаджЪНтОіЮЪЬтЃЌЪєгкжаПМбЙжсЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
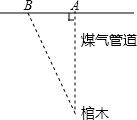 ШчЭМЃЌвЛИіЙХДњЙзФОБЛЬНУїЮЛгкAЕуЕиЯТ24УзДІЃЌгЩгкAЕуЕиУцЯТгаУКЦјЙмЕРЃЌПМЙХШЫдБЯТФмДЙжБЯђЯТЭкОђЃЌЫћУЧБЛдЪаэДгОрAЕу8УзЕФBЕуЭкОђЃЌПМеМШЫдБгІвдгыЕиЦНУцаЮГЩЖрДѓЕФНЧЖШНјааЭкОђВХФмбизюЖЬТЗЯпЭкЕНЙзФОЃПЫћУЧашвЊЭкЖрГЄЕФОрРыЃП
ШчЭМЃЌвЛИіЙХДњЙзФОБЛЬНУїЮЛгкAЕуЕиЯТ24УзДІЃЌгЩгкAЕуЕиУцЯТгаУКЦјЙмЕРЃЌПМЙХШЫдБЯТФмДЙжБЯђЯТЭкОђЃЌЫћУЧБЛдЪаэДгОрAЕу8УзЕФBЕуЭкОђЃЌПМеМШЫдБгІвдгыЕиЦНУцаЮГЩЖрДѓЕФНЧЖШНјааЭкОђВХФмбизюЖЬТЗЯпЭкЕНЙзФОЃПЫћУЧашвЊЭкЖрГЄЕФОрРыЃПВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com