
在平面直角坐标系xOy中,对于点P(x,y),我们把点P(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(3,1),则点A3的坐标为 ,点A2014的坐标为 ;若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
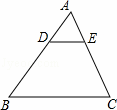
如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E,若线段DE=5,则线段BC的长为( )
|
| A. | 7.5 | B. | 10 | C. | 15 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在平面直角坐标系中,二次函数y=﹣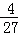 x2+12的图象与y轴交于点A,与x轴交于B,C两点(点B在点C的左侧),连接AB,AC.
x2+12的图象与y轴交于点A,与x轴交于B,C两点(点B在点C的左侧),连接AB,AC.
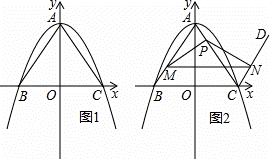
(1)点B的坐标为 ,点C的坐标为 ;
(2)过点C作射线CD∥AB,点M是线段AB上的动点,点P是线段AC上的动点,且始终满足BM=AP(点M不与点A,点B重合),过点M作MN∥BC分别交AC于点Q,交射线CD于点N (点 Q不与点P重合),连接PM,PN,设线段AP的长为n.
①如图2,当n< AC时,求证:△PAM≌△NCP;
AC时,求证:△PAM≌△NCP;
②直接用含n的代数式表示线段PQ的长;
③若PM的长为 ,当二次函数y=﹣
,当二次函数y=﹣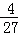 x2+12的图象经过平移同时过点P和点N时,请直接写出此时的二次函数表达式.
x2+12的图象经过平移同时过点P和点N时,请直接写出此时的二次函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE,DE,其中DE交直线AP于点F.

(1)依题意补全图1;
(2)若∠PAB=20°,求∠ADF的度数;
(3)如图2,若45°<∠PAB<90°,用等式表示线段AB,FE,FD之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com