
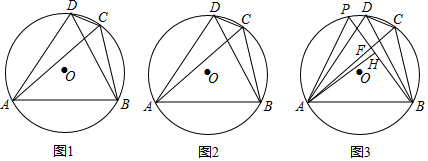
分析 (1)欲证明AD=BD,只要证明∠DAB=∠DBA即可.
(2)如图2中,延长DC到G,使得CG=CB,连接BG.首先证明△ABD,△CBG是等边三角形,再证明△DBG≌△ACB即可.
(3)如图3中,作连接CE,连接AE、BE.首先证明△BEC是等腰直角三角形,由∠PAH=30°,推出PA=2PH,AH=$\sqrt{3}$PH,设PF=a,FH=4x,则BH=21x,FB=25x,推出PA=2(a+4x),AH=$\sqrt{3}$(a+4x),在Rt△AHF中,由AF2=FH2+AH2,推出AF=$\sqrt{(4x)^{2}+[\sqrt{3}(a+4x)]^{2}}$,由△PAF∽△CBF,得$\frac{PA}{CB}$=$\frac{FA}{FB}$,$\frac{2(a+4x)}{5\sqrt{2}}$=$\frac{\sqrt{(4x)^{2}+[\sqrt{3}(a+4x)]^{2}}}{25x}$,即50x2(a+4x)2=16x2+3(a+4x)2 ①,在Rt△ABH中,AH2+BH2=AB2,推出[$\sqrt{3}$(a+4x)]2+(21x)2=(5$\sqrt{3}$)2,即(a+4x)2=25-147x2 ②,解方程组即可解决问题.
解答 (1)证明:如图1中,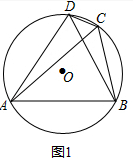
∵∠DCA+∠DCB=180°,又∵∠DCB+∠DAB=180°,
∴∠DCA=∠DAB,
∵∠DCA=∠ABD,
∴∠DAB=∠ABD,
∴DA=BD.
(2)证明:如图2中,延长DC到G,使得CG=CB,连接BG.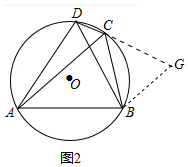
∵∠BCA=60°,
∴∠ADB=∠ACB=60°,∵DA=DB,
∴△ADB是等边三角形,
∴∠DAB=60°,∠DCB=180°-∠DAB=120°,
∴∠BCG=60°,∵CG=CB,
∴△BCG是等边三角形,
∴∠G=∠ACB=60°,∠CAB=∠BDG,
在△DBG和△ACB中,
$\left\{\begin{array}{l}{∠G=∠ACB}\\{∠BDG=∠BAC}\\{AB=BD}\end{array}\right.$,
∵△DBG≌△ACB(ASA),
∴DG=AC,
∴AC=DC+CG=DC+BC.
(3)解:如图3中,作连接CE,连接AE、BE.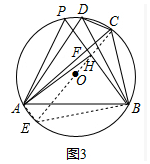
∵△ADB是等边三角形,⊙O半径为5,
∴AB=AD=BD=5$\sqrt{3}$,
∵∠CAE=90°,
∴CE是直径,
∴∠EBC=90°,
∵CD=AE,
∴$\widehat{CD}$=$\widehat{AE}$,
∵$\widehat{DCB}$=$\widehat{AEB}$,
∴$\widehat{BC}$=$\widehat{EB}$,
∴BC=BE,
∵CE=10,
∴EB=BC=5$\sqrt{2}$,
∵∠P=∠ADB=∠ACB=60°,AH⊥PB,
∴∠PAH=30°,
∴PA=2PH,AH=$\sqrt{3}$PH,设PF=a,FH=4x,则BH=21x,FB=25x,
∴PA=2(a+4x),AH=$\sqrt{3}$(a+4x),
在Rt△AHF中,∵AF2=FH2+AH2,
∴AF=$\sqrt{(4x)^{2}+[\sqrt{3}(a+4x)]^{2}}$,
∵∠P=∠ACB=60°,∠PAF=∠CBF,
∴△PAF∽△CBF,
∴$\frac{PA}{CB}$=$\frac{FA}{FB}$,
∴$\frac{2(a+4x)}{5\sqrt{2}}$=$\frac{\sqrt{(4x)^{2}+[\sqrt{3}(a+4x)]^{2}}}{25x}$,
即50x2(a+4x)2=16x2+3(a+4x)2 ①
在Rt△ABH中,AH2+BH2=AB2,
∴[$\sqrt{3}$(a+4x)]2+(21x)2=(5$\sqrt{3}$)2,
即(a+4x)2=25-147x2 ②
把②代入①得50x2(25-147x2)=16x2+75-212x2,
整理得294x4-67x2+3=0,
∴(49x2-3)(6x2-1)=0,
∴x2=$\frac{3}{49}$或(x2=$\frac{1}{6}$不合题意舍弃),
把x2=$\frac{3}{49}$代入②得,(a+4x)2=25-9=16,
∴a+4x=4,
∴2(a+4x)=8.
∴AP=8.
点评 本题考查圆综合题、等腰三角形的判定和性质、等边三角形的判定和性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会利用参数,构建方程,利用方程组解决问题,属于中考压轴题.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:填空题
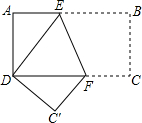 在长方形纸片ABCD中,AD=6cm,AB=8cm,按如图方式折叠,使点B与点D重合,折痕为EF,则EF的长为$\frac{15}{2}$.
在长方形纸片ABCD中,AD=6cm,AB=8cm,按如图方式折叠,使点B与点D重合,折痕为EF,则EF的长为$\frac{15}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,?ABOC如图放置,点C的坐标是(-1,0),点A在y轴的正半轴上,将此平行四边形绕点O顺时针旋转90°,得?A′B′OC′,抛物线y=ax2+bx+4过点C、A、A′,点M是此抛物线的一动点,设点M的横坐标为m.
在平面直角坐标系中,?ABOC如图放置,点C的坐标是(-1,0),点A在y轴的正半轴上,将此平行四边形绕点O顺时针旋转90°,得?A′B′OC′,抛物线y=ax2+bx+4过点C、A、A′,点M是此抛物线的一动点,设点M的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
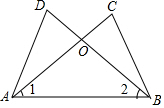 如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件( )
如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件( )| A. | AD=BC | B. | BD=AC | C. | ∠D=∠C | D. | OA=AB |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
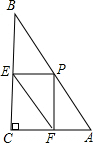 如图,直角三角形ABC中,AC=1,BC=2,P为斜边AB上一动点.PE⊥BC,PF⊥CA,则线段EF长的最小值为$\frac{2}{5}\sqrt{5}$.
如图,直角三角形ABC中,AC=1,BC=2,P为斜边AB上一动点.PE⊥BC,PF⊥CA,则线段EF长的最小值为$\frac{2}{5}\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com