
【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( )
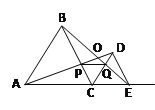
A.①②③④B.②③④⑤C.①③④⑤D.①②③⑤
【答案】D
【解析】
①由于△ABC和△CDE是等边三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,从而证出△ACD≌△BCE,可推知AD=BE;
②由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知②正确;
③根据②△CQB≌△CPA(ASA),可知③正确;
④根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,可知∠DQE≠∠CDE,可知④错误;
⑤利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,可知⑤正确.
解:∵等边△ABC和等边△CDE,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∴①正确,
∵△ACD≌△BCE,
∴∠CBE=∠DAC,
又∵∠ACB=∠DCE=60°,
∴∠BCD=60°,即∠ACP=∠BCQ,
又∵AC=BC,
∴△CQB≌△CPA(ASA),
∴CP=CQ,
又∵∠PCQ=60°可知△PCQ为等边三角形,
∴∠PQC=∠DCE=60°,
∴PQ∥AE②正确,
∵△CQB≌△CPA,
∴AP=BQ③正确,
∵AD=BE,AP=BQ,
∴AD-AP=BE-BQ,
即DP=QE,
∵∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,
∴∠DQE≠∠CDE,故④错误;
∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
∵等边△DCE,
∠EDC=60°=∠BCD,
∴BC∥DE,
∴∠CBE=∠DEO,
∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,
∴⑤正确.
故选:D.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】如图,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)(参考数据:参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)
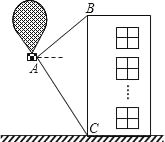
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市扶贫办在精准扶贫工作中,组织30辆汽车装运花椒、核桃、甘蓝向外地销售.按计划30辆车都要装运,每辆汽车只能装运同一种产品,且必须装满,根据下表提供的信息,解答以下问题:
产品名称 | 核桃 | 花椒 | 甘蓝 |
每辆汽车运载量(吨) | 10 | 6 | 4 |
每吨土特产利润(万元) | 0.7 | 0.8 | 0.5 |
若装运核桃的汽车为x辆,装运甘蓝的车辆数是装运核桃车辆数的2倍多1,假设30辆车装运的三种产品的总利润为y万元.
(1)求y与x之间的函数关系式;
(2)若装花椒的汽车不超过8辆,求总利润最大时,装运各种产品的车辆数及总利润最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
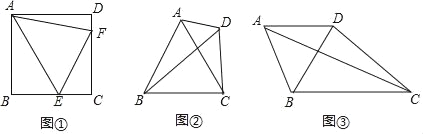
(1)如图①,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,则线段BE、EF、FD之间的数量关系为 ;
(2)如图②,在△ADC中,AD=2,CD=4,∠ADC是一个不固定的角,以AC为边向△ADC的另一侧作等边△ABC,连接BD,则BD的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;
问题解决
(3)如图③,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4![]() ,若BD⊥CD,垂足为点D,则对角线AC的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由.
,若BD⊥CD,垂足为点D,则对角线AC的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知![]() ,点P在OA上,且
,点P在OA上,且![]() ,点P关于直线OB的对称点是Q,则
,点P关于直线OB的对称点是Q,则![]() ________.
________.
(2)已知![]() ,点P在
,点P在![]() 的内部,
的内部,![]() ,点
,点![]() 和点P关于OA对称,点
和点P关于OA对称,点![]() 和点P关于OB对称,则
和点P关于OB对称,则![]() 、O、
、O、![]() 三点构成的三角形是________三角形,其周长为________.
三点构成的三角形是________三角形,其周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“若矩形的两边长分别为3和4,求矩形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”,等等.
(1)设A=![]() ,B=
,B=![]() ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com