
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为200人 B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选F的人数为35人 D. 被调查的学生中最想选D的有55人
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:
【题目】(1)发现:
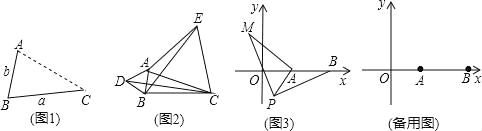
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:
如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE. 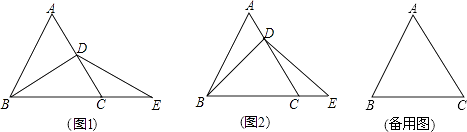
(1)若点D是AC的中点,如图1,求证:AD=CE.
(2)若点D不是AC的中点,如图2,试判断AD与CE的数量关系,并证明你的结论:(提示:过点D作DF∥BC,交AB于点F.)
(3)若点D在线段AC的延长线上,(2)中的结论是否仍成立?如果成立,给予证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD点于点F. 
(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测,整理样本数据,并结合2010年抽样结果,得到下列统计图: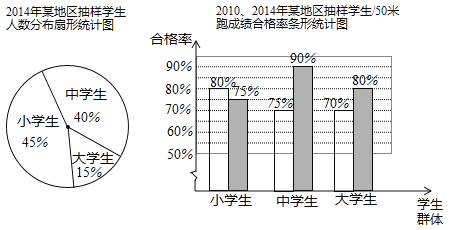
(1)本次检测抽取了大、中、小学生共 名,其中小学生 名;
(2)根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为 名;
(3)比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆. 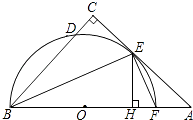
(1)求证:AC是⊙O的切线.
(2)过点E作EH⊥AB于点H,求证:CD=HF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以BC为直径的圆交△ABC的两边AB、AC于点D、E,点E恰为AC的中点,BF为△ABC的外角平分线,点F在圆上,请你仅用一把无刻度的直尺,过点A作一条线段,将△ABC分成面积相等的两部分. 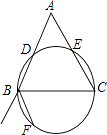
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABFG和正方形CDEF的顶点在边长为1的正方形网格的格点上.
(1)建立平面直角坐标系,使点B,C的坐标分别为(0,0)和(5,0),并写出点A,D,E,F,G的坐标;
(2)连接BE和CG相交于点H,BE和CG相等吗?并计算∠BHC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com