
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
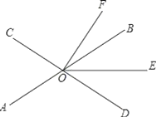
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
【答案】(1)55°(2)①![]() x②100°
x②100°
【解析】
(1)由对顶角的性质可知∠BOD=70°,从而可求得∠FOB=20°,由角平分线的定义可知∠BOE=![]() ∠BOD,最后根据∠EOF=∠BOE+∠FOB求解即可;
∠BOD,最后根据∠EOF=∠BOE+∠FOB求解即可;
(2)①先证明∠AOE=∠COE= x°,然后由角平分线的定义可知∠FOE=![]() x°;
x°;
②∠BOE=∠FOE-∠FOB可知∠BOE=![]() x°-15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.
x°-15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.
解:(1)由对顶角相等可知:∠BOD=∠AOC=70°,
∵∠FOB=∠DOF-∠BOD,
∴∠FOB=90°-70°=20°,
∵OE平分∠BOD,
∴∠BOE=![]() ∠BOD=
∠BOD=![]() ×70°=35°,
×70°=35°,
∴∠EOF=∠FOB+∠BOE=35°+20°=55°;
(2)①∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,
∴∠COE=∠AOE=x°,
∵OF平分∠COE,
∴∠EOF=![]() x°;
x°;
②∵∠BOE=∠FOE-∠FOB,
∴∠BOE=![]() x°-15°,
x°-15°,
∵∠BOE+∠AOE=180°,
∴![]() x°-15°+x°=180°,解得:x=130,
x°-15°+x°=180°,解得:x=130,
∴∠AOC=2∠BOE=2×(180°-130°)=100°.


科目:初中数学 来源: 题型:
【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
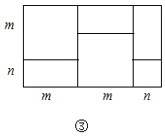
【题目】如图①是一个长为![]() 、宽为
、宽为![]() 的长方形,沿图中虛线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
的长方形,沿图中虛线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
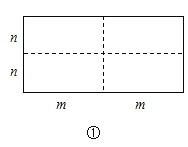
(1)图②中的阴影部分的面积为
(2)观察图②,请你写出代数式![]() 与
与![]() 之间的等量关系式
之间的等量关系式

(3)若![]() 则
则![]()
(4)实际上有许多代数恒等式可以用图形的面积来表示.如图③,它表示
(5)试画出一个几何图形,使它的面积能表示![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xoy中,一次函数y= ![]() x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.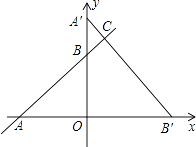
(1)求直线A′B′的解析式;
(2)若直线A′B′与直线AB相交于点C,求S△ABC:S△ABO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P,根据下列条件,求∠BPC的度数.
(1)若∠ABC=50°,∠ACB=60°,则∠BPC= ;
(2)若∠ABC+∠ACB=120°,则∠BPC= ;
(3)若∠A=80°,则∠BPC= ;
(4)从以上的计算中,你能发现已知∠A,求∠BPC的公式是:∠BPC= (提示:用∠A表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为节约能源,某单位按以下规定收取每月电费:用电不超过140度,按每度![]() 元收费,如果超过140度,超过部分按每度
元收费,如果超过140度,超过部分按每度![]() 元收费.
元收费.
![]() 若某住户六月份的用电量是130度,该用户六月份应缴多少电费?
若某住户六月份的用电量是130度,该用户六月份应缴多少电费?
![]() 若该住户七月份的用电量是200度,该用户七月份应缴多少电费?
若该住户七月份的用电量是200度,该用户七月份应缴多少电费?
![]() 若某住户十月份的用电量是a度,该用户十月份应缴多少电费?
若某住户十月份的用电量是a度,该用户十月份应缴多少电费?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com