
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,AD、BE相交于点![]() ,且BF=AC.
,且BF=AC.
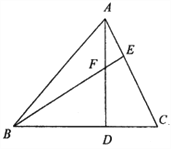
(1)求证:△ADC≌△BDF
(2)若CD=3,BD=5,求AF的长.
【答案】(1)证明见解析;(2)AF=2.
【解析】(1)先证明AD=BD,再证明∠FBD=∠DAC,从而利用ASA证明△BDF≌△ADC;
(2)利用全等三角形对应边相等得出DF=CD=4,根据勾股定理求出CF即可.
解:(1)证明:∵AD⊥BC,BE⊥AC,
∴∠FDB=∠CDA=∠AEF=90°.
∵∠FBD+∠FDB+∠BFD=180°,
∠CAD+∠AEF+∠AFE=180°,
又∵∠BFD=∠AFE,
∴ ∠FBD = ∠CAD.
∵在△ADC和△BDF中,
∠FDB=∠CDA ,
∠FBD = ∠CAD ,
BF=AC,
∴ △ADC≌△BDF(AAS).
(2) 解:∵ 由(1)知,
△ADC≌△BDF,
∴ DC=DF,AD=BD,
∴ AF=AD-DF=BD-CD=5-3=2.
“点睛”此题主要考查了全等三角形的判定和性质,勾股定理的应用,关键是找出能使三角形全等的条件,注意:全等三角形的判定定理有SAS、ASA、AAS、SSS,全等三角形的对应角相等,对应边相等.


科目:初中数学 来源: 题型:
【题目】下列调查适合全面调查的是( )
A. 了解七(1)班“500米跑”的成绩 B. 了解一批灯泡的使用寿命.
C. 了解一批导弹的杀伤半径. D. 了解一批袋装食品是否含有防腐剂.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“十一”长假期间平均每天的营业额是15万元,由此推算10月份的总营业额约为15×31=465(万元),你认为这样推断是否合理?答:________________.(选填“合理”或“不合理”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班组织20名同学去春游,同时租用两种型号的车辆,一种车每辆有8个座位,另一种车每辆有4个座位,要求租用的车辆不留空座,也不能超载。租车方案有( )
A. 4种 B. 3种 C. 2种 D. 1种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用语言叙述多项式“-a-3”所表示的数量关系,下列叙述正确的是( )
A. a与-3的和
B. a的相反数与3的差
C. a的相反数与3的和
D. a的相反数与-3的差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)经过6秒后,BP= cm,BQ= cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于![]() cm2?
cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班有20位同学参加乒乓球、羽毛球比赛,甲说:“只参加一项的人数大于14人。”乙说:“两项都参加的人数小于5人。”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )
A. 若甲对,则乙对 B. 若乙对,则甲对
C. 若乙错,则甲错 D. 若甲错,则乙对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com