
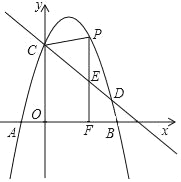
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=Љx2+bx+cгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉКЭЕуBЃЌгыyжсНЛгкCЃЈ0ЃЌ3ЃЉЃЌжБЯпy=![]() +mОЙ§ЕуCЃЌгыХзЮяЯпЕФСэвЛНЛЕуЮЊЕуDЃЌЕуPЪЧжБЯпCDЩЯЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPFЁЭxжсгкЕуFЃЌНЛжБЯпCDгкЕуEЃЌЩшЕуPЕФКсзјБъЮЊmЃЎ
+mОЙ§ЕуCЃЌгыХзЮяЯпЕФСэвЛНЛЕуЮЊЕуDЃЌЕуPЪЧжБЯпCDЩЯЗНХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPFЁЭxжсгкЕуFЃЌНЛжБЯпCDгкЕуEЃЌЩшЕуPЕФКсзјБъЮЊmЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНВЂЧѓГіЕуDЕФзјБъЃЛ
ЃЈ2ЃЉСЌНгPDЃЌЁїCDPЕФУцЛ§ЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧыЧѓГіУцЛ§ЕФзюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБЁїCPEЪЧЕШбќШ§НЧаЮЪБЃЌЧыжБНгаДГіmЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љx2+2x+3ЃЌDЕузјБъЮЊЃЈ![]() ЃЉЃЛЃЈ2ЃЉЕБm=
ЃЉЃЛЃЈ2ЃЉЕБm=![]() ЪБЃЌЁїCDPЕФУцЛ§ДцдкзюДѓжЕЃЌзюДѓжЕЮЊ
ЪБЃЌЁїCDPЕФУцЛ§ДцдкзюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЛЃЈ3ЃЉmЕФжЕЮЊ
ЃЛЃЈ3ЃЉmЕФжЕЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓХзЮяЯпНтЮіЪНКЭжБЯпCDЕФНтЮіЪНЃЌШЛКѓНтЗНГЬзщ ЕУDЕузјБъЃЛ
ЕУDЕузјБъЃЛ
ЃЈ2ЃЉЩшPЃЈmЃЌ-m2+2m+3ЃЉЃЌдђEЃЈmЃЌ-![]() m+3ЃЉЃЌдђPE=-m2+
m+3ЃЉЃЌдђPE=-m2+![]() mЃЌРћгУШ§НЧаЮУцЛ§ЙЋЪНЕУЕНSЁїPCD=
mЃЌРћгУШ§НЧаЮУцЛ§ЙЋЪНЕУЕНSЁїPCD=![]() ЁС
ЁС![]() ЁСЃЈ-m2+
ЁСЃЈ-m2+![]() mЃЉ=-
mЃЉ=-![]() m2+
m2+![]() mЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЛ
mЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЬжТлЃКЕБPC=PEЪБЃЌm2+ЃЈ-m2+2m+3-3ЃЉ2=ЃЈ-m2+![]() mЃЉ2ЃЛЕБCP=CEЪБЃЌm2+ЃЈ-m2+2m+3-3ЃЉ2=m2+ЃЈ-
mЃЉ2ЃЛЕБCP=CEЪБЃЌm2+ЃЈ-m2+2m+3-3ЃЉ2=m2+ЃЈ-![]() m+3-3ЃЉ2ЃЛЕБEC=EPЪБЃЌm2+ЃЈ-
m+3-3ЃЉ2ЃЛЕБEC=EPЪБЃЌm2+ЃЈ-![]() m+3-3ЃЉ2=ЃЈ-m2+
m+3-3ЃЉ2=ЃЈ-m2+![]() mЃЉ2ЃЌШЛКѓЗжБ№НтЗНГЬМДПЩЕУЕНТњзуЬѕМўЕФmЕФжЕЃЎ
mЃЉ2ЃЌШЛКѓЗжБ№НтЗНГЬМДПЩЕУЕНТњзуЬѕМўЕФmЕФжЕЃЎ
ЃЈ1ЃЉАбAЃЈЉ1ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉЗжБ№ДњШыy=Љx2+bx+cЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=Љx2+2x+3ЃЛ
АбCЃЈ0ЃЌ3ЃЉДњШыy=Љ![]() x+nЃЌНтЕУn=3ЃЌ
x+nЃЌНтЕУn=3ЃЌ
ЁржБЯпCDЕФНтЮіЪНЮЊy=Љ![]() x+3ЃЌ
x+3ЃЌ
НтЗНГЬзщ ЃЌНтЕУ
ЃЌНтЕУ![]()
Лђ![]() ЃЌ
ЃЌ
ЁрDЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ2ЃЉДцдкЃЎ
ЩшPЃЈmЃЌЉm2+2m+3ЃЉЃЌдђEЃЈmЃЌЉ![]() m+3ЃЉЃЌ
m+3ЃЉЃЌ
ЁрPE=Љm2+2m+3ЉЃЈЉ![]() m+3ЃЉ=Љm2+
m+3ЃЉ=Љm2+![]() mЃЌ
mЃЌ
ЁрSЁїPCD=![]()
![]() ЃЈЉm2+
ЃЈЉm2+![]() mЃЉ=Љ
mЃЉ=Љ![]() m2+
m2+![]() m=Љ
m=Љ![]() ЃЈmЉ
ЃЈmЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЕБm=![]() ЪБЃЌЁїCDPЕФУцЛ§ДцдкзюДѓжЕЃЌзюДѓжЕЮЊ
ЪБЃЌЁїCDPЕФУцЛ§ДцдкзюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБPC=PEЪБЃЌm2+ЃЈЉm2+2m+3Љ3ЃЉ2=ЃЈЉm2+![]() mЃЉ2ЃЌНтЕУm=0ЃЈЩсШЅЃЉЛђm=
mЃЉ2ЃЌНтЕУm=0ЃЈЩсШЅЃЉЛђm=![]() ЃЛ
ЃЛ
ЕБCP=CEЪБЃЌm2+ЃЈЉm2+2m+3Љ3ЃЉ2=m2+ЃЈЉ![]() m+3Љ3ЃЉ2ЃЌНтЕУm=0ЃЈЩсШЅЃЉЛђm=
m+3Љ3ЃЉ2ЃЌНтЕУm=0ЃЈЩсШЅЃЉЛђm=![]() ЃЈЩсШЅЃЉЛђm=
ЃЈЩсШЅЃЉЛђm=![]() ЃЛ
ЃЛ
ЕБEC=EPЪБЃЌm2+ЃЈЉ![]() m+Љ3ЃЉ2=ЃЈЉm2+
m+Љ3ЃЉ2=ЃЈЉm2+![]() mЃЉ2ЃЌНтЕУm=
mЃЉ2ЃЌНтЕУm=![]() ЃЈЩсШЅЃЉЛђm=
ЃЈЩсШЅЃЉЛђm=![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌmЕФжЕЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
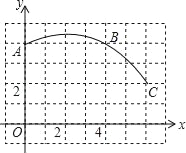
ЁОЬтФПЁПШчЭМЃЌдкЕЅЮЛГЄЖШЮЊ1ЕФе§ЗНаЮЭјИёжаНЈСЂвЛжБНЧзјБъЯЕЃЌвЛЬѕдВЛЁОЙ§ЭјИёЕуAЁЂBЁЂCЃЌЭъГЩЯТСаЮЪЬтЃК
ЃЈ1ЃЉдкЭМжаБъГідВаФDЃЌдђдВаФDЕуЕФзјБъЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉСЌНгADЁЂCDЃЌдђЁЯADCЕФЖШЪ§ЮЊЁЁ ЁЁЃЛ
ЃЈ3ЃЉШєЩШаЮDACЪЧвЛИідВзЖЕФВрУцеЙПЊЭМЃЌЧѓИУдВзЖЕзУцАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГпЙцзїЭМвЊЧѓЃКЂёЁЂЙ§жБЯпЭтвЛЕузїетЬѕжБЯпЕФДЙЯпЃЛЂђЁЂзїЯпЖЮЕФДЙжБЦНЗжЯпЃЛ
ЂѓЁЂЙ§жБЯпЩЯвЛЕузїетЬѕжБЯпЕФДЙЯпЃЛЂєЁЂзїНЧЕФЦНЗжЯпЃЎ
ШчЭМЪЧАДЩЯЪівЊЧѓХХТвЫГађЕФГпЙцзїЭМЃК
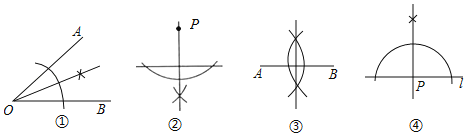
дђе§ШЗЕФХфЖдЪЧЃЈЁЁЁЁЃЉ
A. ЂйЉЂєЃЌЂкЉЂђЃЌЂлЉЂёЃЌЂмЉЂѓ B. ЂйЉЂєЃЌЂкЉЂѓЃЌЂлЉЂђЃЌЂмЉЂё
C. ЂйЉЂђЃЌЂкЉЂєЃЌЂлЉЂѓЃЌЂмЉЂё D. ЂйЉЂєЃЌЂкЉЂёЃЌЂлЉЂђЃЌЂмЉЂѓ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
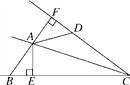
ЁОЬтФПЁПШчЭМЃЌACЦНЗжЁЯBCDЃЌABЃНADЃЌAEЁЭBCгкEЃЌAFЁЭCDгкF.
(1)ШєЁЯABEЃН60ЁуЃЌЧѓЁЯCDAЕФЖШЪ§ЃЛ
(2)ШєAEЃН2ЃЌBEЃН1ЃЌCDЃН4.ЧѓЫФБпаЮAECDЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
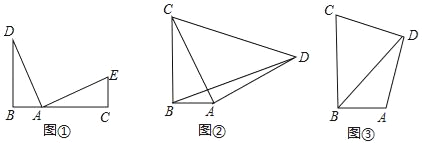
ЁОЬтФПЁПЃЈ1ЃЉЙлВьВТЯы
ШчЭМЂйЕуBЁЂAЁЂCдкЭЌвЛЬѕжБЯпЩЯЃЌDBЁЭBCЃЌECЁЭBCЧвЁЯDAE=90ЁуЃЌAD=AEЃЌдђBCЁЂBDЁЂCEжЎМфЕФЪ§СПЙиЯЕЮЊЃЛ
ЃЈ2ЃЉЮЪЬтНтОі
ШчЭМЂкЃЌдкRtЁїABCжаЃЌЁЯABC=90ЁуЃЌCB=4ЃЌAB=2ЃЌвдACЮЊжБНЧБпЯђЭтзїЕШбќRtЁїDACЃЌСЌНсBDЃЌЧѓBDЕФГЄЃЛ
ЃЈ3ЃЉЭиеЙбгЩь
ШчЭМЂлЃЌдкЫФБпаЮABCDжаЃЌЁЯABC=ЁЯADC=90ЁуЃЌCB=4ЃЌAB=2ЃЌDC=DAЃЌЧыжБНгаДГіBDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯШдФЖСШЛКѓНтОіЮЪЬтЃК
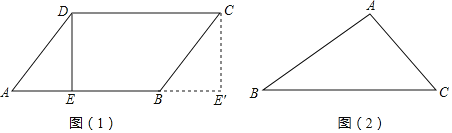
ЃЈдФЖСЃЉШчЭМЃЈ1ЃЉЃЌдкABCDжаЃЌЙ§ЕуDзїDEЁЭABгкЕуEбиDEЯпНЋЁїDEAМєЧаЯТРДЃЌВЂЦНвЦЁїDEAЃЌЪЙЦфЦДНгдкЁїCEЁфBДІетбљЃЌдРДABCDОЭБфГЩвЛИіОиаЮEEЁфCDЃЎ
ЃЈЮЪЬтНтОіЃЉШчЭМЃЈ2ЃЉЃЌНЋЁїABCЭЈЙ§МєЧаКЭЦДНгЃЌЕУЕНвЛИіОиаЮЃЎвЊЧѓЃК
ЃЈ1ЃЉМєЧаЯпгУЪЕЯпЃЌЦДНгЭМгУащЯпЃЛ
ЃЈ2ЃЉЫЕУїМєЯТЕФЭМаЮЪЧдѕбљдЫЖЏЦДНгЕФЃЛ
ЃЈ3ЃЉМгзЂБивЊЕФзжФИЃЌЦДНгКѓЕФЗЧжиКЯзжФИдкдзжФИЕФгвЩЯНЧБъзЂЁАЁфЁБЃЌШчЃКEЁф
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
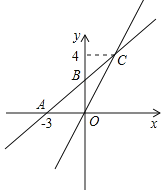
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§yЃНkx+bЕФЭМЯѓгыxжсНЛгкЕуAЃЈЉ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуBЃЌЧвгые§БШР§КЏЪ§yЃН![]() xЕФЭМЯѓНЛЕуЮЊCЃЈmЃЌ4ЃЉЃЎ
xЕФЭМЯѓНЛЕуЮЊCЃЈmЃЌ4ЃЉЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§yЃНkx+bЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїBOCЕФУцЛ§ЃЛ
ЃЈ3ЃЉШєЕуDдкЕкЖўЯѓЯоЃЌЁїDABЮЊЕШбќжБНЧШ§НЧаЮЃЌдђЕуDЕФзјБъЮЊЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИпЖћЗђдЫЖЏдБНЋвЛИіаЁЧђбигыЕиУцГЩвЛЖЈНЧЖШЕФЗНЯђЛїГіЃЌдкВЛПМТЧПеЦјзшСІЕФЬѕМўЯТЃЌаЁЧђЕФЗЩааИпЖШhЃЈmЃЉгыЫќЕФЗЩааЪБМфЃЈsЃЉТњзуЖўДЮКЏЪ§ЙиЯЕЃЌtгыhЕФМИзщЖдгІжЕШчЯТБэЫљЪОЃК
tЃЈsЃЉ | 0 | 0.5 | 1 | 1.5 | 2 | Ё |
hЃЈmЃЉ | 0 | 8.75 | 15 | 18.75 | 20 | Ё |
ЃЈ1ЃЉЧѓhгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДtЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ2ЃЉЧѓаЁЧђЗЩаа3sЪБЕФИпЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпy=ax2+bx+3ЃЈaЁй0ЃЉЙ§AЃЈ4ЃЌ4ЃЉЃЌBЃЈ2ЃЌmЃЉСНЕуЃЌЕуBЕНХзЮяЯпЖдГЦжсЕФОрРыМЧЮЊdЃЌТњзу0ЃМdЁм1ЃЌдђЪЕЪ§mЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
A. mЁм2ЛђmЁн3 B. mЁм3ЛђmЁн4 C. 2ЃМmЃМ3 D. 3ЃМmЃМ4
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com