
【题目】已知α是锐角,且sin(α﹣15°)= ![]() 计算:
计算: ![]() ﹣4cosα﹣(π﹣3.14)0+tanα+(
﹣4cosα﹣(π﹣3.14)0+tanα+( ![]() )﹣1的值.
)﹣1的值.
【答案】解:∵sin(α﹣15°)= ![]() ,
,
∴α﹣15°=30°,
则α=45°,
![]() ﹣4cosα﹣(π﹣3.14)0+tanα+(
﹣4cosα﹣(π﹣3.14)0+tanα+( ![]() )﹣1
)﹣1
=2 ![]() ﹣4×
﹣4× ![]() ﹣1+1+3
﹣1+1+3
=3.
【解析】首先利用特殊角的三角函数值得出α的度数,再利用负整数指数幂的性质以及零指数幂的性质和特殊角的三角函数值分别化简得出答案.
【考点精析】通过灵活运用零指数幂法则和整数指数幂的运算性质,掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)即可以解答此题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
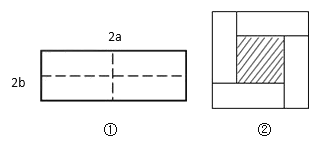
(1)图②中的阴影部分的正方形的边长等于 .(用含![]() ,
,![]() 的代数式表示)
的代数式表示)
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积:
方法①: .
方法②: .
(3)观察图②,直接写出![]() 、
、![]() 、
、![]() 这三个代数式之间的等量关系.
这三个代数式之间的等量关系.
(4)根据(3)题中的等量关系,若![]() ,
,![]() ,求图②中阴影部分的面积.
,求图②中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
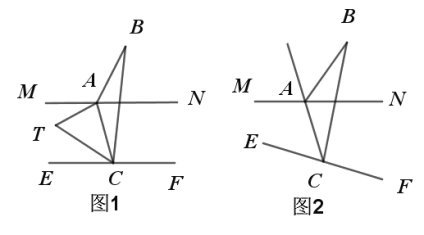
【题目】已知点A和点C分别在直线MN和直线EF上,点B在直线外,∠BAN=α,∠BCF=β.
(1)如图1,若MN∥EF,则∠B= (用α,β的式子表示,不写证明过程)
(2)在(1)的条件下,点T在直线MN与直线EF之间,∠MAT=![]() ∠BAN,∠TCB=2∠TCE,求∠B与∠T之间的数量关系.
∠BAN,∠TCB=2∠TCE,求∠B与∠T之间的数量关系.
(3)如图2,若MN不平行于EF,直线AC平分∠MAB,且平分∠ECB,则∠B= (用α,β的式子表示,不写证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列4个命题:①两边及其中一边上的中线对应相等的两个三角形全等;②两边及其中一边上的高对应相等的两个三角形全等;③两边及一角对应相等的两个三角形全等;④有两角及其中一角的角平分线对应相等的两个三角形全等.其中正确的的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
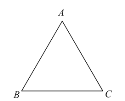
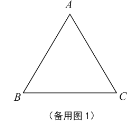
【题目】如图,在等边![]() 中,边
中,边![]() 厘米,若动点
厘米,若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为1厘米/秒,设点
的路径运动,且速度为1厘米/秒,设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
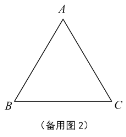
(1)当![]() 时,判断
时,判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当![]() 的面积为
的面积为![]() 面积的一半时,求
面积的一半时,求![]() 的值;
的值;
(3)另有一点![]() ,从点
,从点![]() 开始,按
开始,按![]() 的路径运动,且速度为
的路径运动,且速度为![]() 厘米/秒,若
厘米/秒,若![]() 、
、![]() 两点同时出发,当
两点同时出发,当![]() 、
、![]() 中有一点到达终点时,另一点也停止运动.当
中有一点到达终点时,另一点也停止运动.当![]() 为何值时,直线
为何值时,直线![]() 把
把![]() 的周长分成相等的两部分.
的周长分成相等的两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校创新能力大赛的笔试情况,随机抽查了部分参赛同学的成绩,整理井制作了不完整的统计表和统计图,请根据图表中提供的信息解答问题:
分数x(分) | 频数 | 百分比 |
60≤x<70 | 30 | 10% |
70≤x<80 | 90 | n |
80≤x<90 | m | 40% |
90≤x<100 | 60 | 20% |
(1)本次调查统计的学生人数为多少.
(2)在表中:写出m,n的值.
(3)补全频数分布直方图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.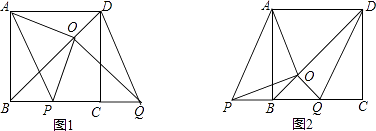
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB , BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y= ![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.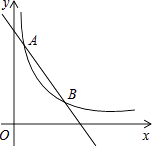
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com