
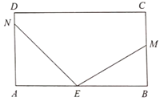
【题目】如图,长方形纸片ABCD,点E在边AB上,M、N分别在射线BC和射线AD上,连接EM,EN,将三角形MBE沿EM折叠(把物体的一部分翻转和另一部分贴拢),点B落在点B’处;将三角形NAE沿EN折叠,点A落在点A’处.
(1)若![]() ,
,![]() ,用直尺、量角器画出射线EB’与EA’;
,用直尺、量角器画出射线EB’与EA’;
(2)若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的度数.
的度数.
【答案】(1)作图见解析;(2)30°;(3)∠A'EB'=180°-2(α+β)或2(α+β)-180°.
【解析】
(1)根据已知作图即可;
(2)由折叠的性质得到∠AEN=∠A'EN,∠BEM=∠B'EM,根据平角的定义得到2∠AEN+2∠BEM+∠A'EB'=180°,即可得到结论;
(3)分两种情况讨论:①当α+β≤90°时,②当α+β>90°时.
(1)如图:
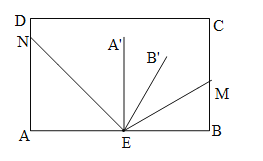
(2)由折叠的性质得:∠AEN=∠A'EN,∠BEM=∠B'EM.
∵2∠AEN+2∠BEM+∠A'EB'=180°,
∴∠A'EB'=180°-2(∠AEN+∠BEM)=180°-2(45°+30°)=30°;
(3)分两种情况讨论:
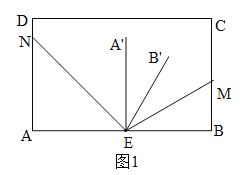
①当α+β≤90°时,如图1,由(2)可知:∠A'EB'=180°-2(∠AEN+∠BEM)=180°-2(α+β);
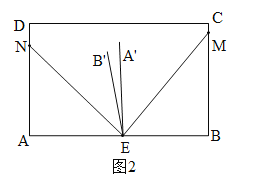
②当α+β>90°时,如图2,类似可得:∠A'EB'=2(∠AEN+∠BEM)-180°=2(α+β)-180°.
综上所述:∠A'EB'=180°-2(α+β)或2(α+β)-180°.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c(b、c是常数)与x轴有两个交点,其中有一点的坐标为A(1,0),点P(m,t)(m≠0)为抛物线上的一个动点.
(1)设y′=m+t,写出y′关于m的函数解析式,并求出该函数图象的对称轴(用含c的代数式表示);
(2)在(1)的条件下,当m≤3时,与其对应的函数y′的最小值为﹣![]() ,求抛物线y=x2+bx+c的解析式;
,求抛物线y=x2+bx+c的解析式;
(3)在(2)的条件下,P点关于原点的对称点为P′,且P′落在第一象限内,当P′A2取得最小值时,求m与t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长方体的表面展开图,每个外表面都标注了字母,请根据要求回答问题:
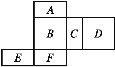
(1)如果面A在多面体的底部,那么哪一个面会在上面?
(2)如果面F在前面,从左面看是面B,那么哪一个面会在上面?
(3)如果从右面看是面C,面D在后面,那么哪一个面会在上面?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
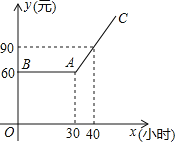
(1)若小李11月份上网20小时,他应付多少元的上网费用?
(2)当x≥30,求y与x之间的函数关系式;
(3)若小李12月份上网费用为135元,则他在该月份的上网时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
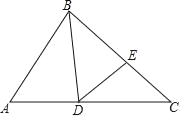
【题目】如图,BD是△ABC的角平分线,点E位于边BC上,已知BD是BA与BE的比例中项.
(1)求证:∠CDE=![]() ∠ABC;
∠ABC;
(2)求证:ADCD=ABCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
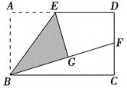
【题目】如图,在矩形ABCD中,点E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=6,BC=4![]() ,则FD=__________.
,则FD=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
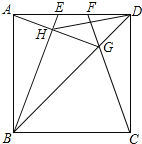
【题目】如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于H.已知正方形ABCD的边长为4cm,解决下列问题:
(1)求证:BE⊥AG;
(2)求线段DH的长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上A. B两点对应的数分别为4和2,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A.点B的距离相等,写出点P对应的数;
(2)数轴上是否存在点P,使点P到点A. 点B的距离之和为10?若存在,求出x的值;若不存在,请说明理由;
(3)若点A点B和点P(点P在原点)同时向右运动,它们的速度分别为2、1、1个长度单位/分,问:多少分钟后P点到点A点B的距离相等?(直接写出结果)
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com