
ЎѕМвДїЎїОЄБЛЅвѕЕДкј¶С§ЙъМеУэЛ®ЖЅЈ¬С§РЈ¶ФѕЕДкј¶И«МеС§ЙъЅшРРБЛМеУэІвКФЈ¬ІўґУјЧЎўТТБЅ°аЦРёчЛж»ъійИЎ![]() ГыС§ЙъіЙјЁ(Въ·Ц
ГыС§ЙъіЙјЁ(Въ·Ц![]() ·Ц)ЅшРРХыАн·ЦОц(іЙјЁµГ·ЦУГ
·Ц)ЅшРРХыАн·ЦОц(іЙјЁµГ·ЦУГ![]() ±нКѕЈ¬№І·ЦіЙЛДЧй:
±нКѕЈ¬№І·ЦіЙЛДЧй:![]()
![]() Ј»
Ј»![]()
![]() Ј¬
Ј¬![]()
![]() )ПВГжёшіцБЛІї·ЦРЕПў:
)ПВГжёшіцБЛІї·ЦРЕПў:
јЧ°а![]() ГыС§ЙъМеУэіЙјЁ:
ГыС§ЙъМеУэіЙјЁ:![]()
ТТ°а![]() ГыС§ЙъМеУэіЙјЁФЪ
ГыС§ЙъМеУэіЙјЁФЪ![]() ЧйЦРµДКэѕЭКЗ:
ЧйЦРµДКэѕЭКЗ: ![]()
јЧЎўТТБЅ°а±»ійИЎС§ЙъМеУэіЙјЁНіјЖ±н
ЖЅѕщКэ | ЦРО»Кэ | ЦЪКэ | ·ЅІо | |
јЧ°а |
|
|
|
|
ТТ°а |
|
|
|
|
ёщѕЭТФЙПРЕПўЈ¬ЅвґрПВБРОКМв:
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј»
Ј»
![]() ёщѕЭТФЙПКэѕЭЈ¬ДгИПОЄ °а(МоЎ°јЧЎ±»тЎ°ТТЎ±)МеУэЛ®ЖЅёьёЯЈ¬ЛµГчАнУЙ(БЅМхАнУЙ):
ёщѕЭТФЙПКэѕЭЈ¬ДгИПОЄ °а(МоЎ°јЧЎ±»тЎ°ТТЎ±)МеУэЛ®ЖЅёьёЯЈ¬ЛµГчАнУЙ(БЅМхАнУЙ):
![]() Ј»
Ј»
![]() .
.
![]() ѧУѕЕДкј¶С§Йъ№І
ѧУѕЕДкј¶С§Йъ№І![]() ИЛЈ¬№АјЖИ«Дкј¶МеУэіЙјЁУЕРг
ИЛЈ¬№АјЖИ«Дкј¶МеУэіЙјЁУЕРг![]() µДС§ЙъИЛКэКЗ¶аЙЩЈї
µДС§ЙъИЛКэКЗ¶аЙЩЈї
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј»ЈЁ2Ј©јЧЈ¬ПкјыЅвОцЈ»ЈЁ3Ј©№АјЖИ«Дкј¶МеУэіЙјЁУЕРгµДС§ЙъФјУР
Ј»ЈЁ2Ј©јЧЈ¬ПкјыЅвОцЈ»ЈЁ3Ј©№АјЖИ«Дкј¶МеУэіЙјЁУЕРгµДС§ЙъФјУР![]() ИЛ
ИЛ
ЎѕЅвОцЎї
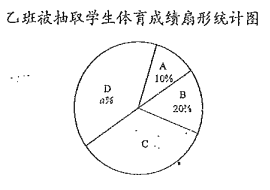
ЈЁ1Ј©ёщѕЭCЧйµДИЛКэЗуµГCЧйЛщХј°Щ·Ц±ИЈ¬ґУ¶шјЖЛгDЧйЛщХј°Щ·Ц±ИЗуaЈ¬ёщѕЭЦРО»КэєНЦЪКэµДёЕДоЗуіцcЎўdЈ»
ЈЁ2Ј©ёщѕЭЖЅѕщКэєНЦРО»КэµДРФЦКЅвґрЈ»
ЈЁ3Ј©УГСщ±ѕ№АјЖЧЬМеЈ¬јЖЛгµГґр°ёЈ®
ЅвЈєЈЁ1Ј©CЧйЛщХј°Щ·Ц±ИЈє![]() ЎБ100%=30%Ј¬
ЎБ100%=30%Ј¬
1Ј10%Ј20%Ј30%=40%Ј¬
Ўаa=40Ј¬
ЎЯТТЧй20ГыС§ЙъµДМеУэіЙјЁµДЦРО»КэКЗґУРЎµЅґуЕЕРтєуЈ¬µЪ10ёцєНµЪ11ёцКэѕЭµДЖЅѕщКэЈ¬ХвБЅёцКэФЪCЧйЈ¬
Ўаb=![]() Ј¬
Ј¬
ЎЯФЪјЧЧй20ГыС§ЙъµДМеУэіЙјЁЦР48іцПЦµДґОКэЧо¶аЈ¬
Ўаc=48Ј»
ЈЁ2Ј©јЧЈ¬АнУЙИзПВЈє
ўЩјЧ°аЖЅѕщ·Ц43.8ґуУЪТТ°аЖЅѕщ·Ц42.5Ј¬јЧ°аЖЅѕщЛ®ЖЅёьёЯЈ¬
ўЪјЧ°аЦРО»Кэ45.5ґуУЪТТ°аЦРО»Кэ42.5Ј¬јЧ°аЦРјдЛ®ЖЅёьёЯЈ»ЈЁґр°ёІ»ОЁТ»Ј¬єПАнјґїЙЈ©
ЈЁ3Ј©20ЎБ40%=8ЈЁИЛЈ©Ј¬![]() (ИЛ)Ј¬
(ИЛ)Ј¬
ґрЈє№АјЖИ«Дкј¶МеУэіЙјЁУЕРгµДС§ЙъФјУР570ИЛЈ®


 ГїїО±ШБ·ПµБРґр°ё
ГїїО±ШБ·ПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
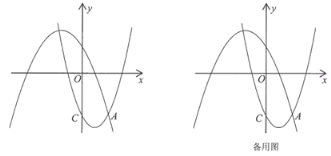
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµxOyЦРЈ¬ЕЧОпПЯL1Јє![]() №эµгC(0Ј¬©Ѓ3)Ј¬УлЕЧОпПЯL2Јє
№эµгC(0Ј¬©Ѓ3)Ј¬УлЕЧОпПЯL2Јє![]() µДТ»ёцЅ»µгОЄAЈ¬ЗТµгAµДєбЧш±кОЄ2Ј¬µгPЎўQ·Ц±рКЗЕЧОпПЯL1ЎўЕЧОпПЯL2ЙПµД¶ЇµгЈ®
µДТ»ёцЅ»µгОЄAЈ¬ЗТµгAµДєбЧш±кОЄ2Ј¬µгPЎўQ·Ц±рКЗЕЧОпПЯL1ЎўЕЧОпПЯL2ЙПµД¶ЇµгЈ®
ЈЁ1Ј©ЗуЕЧОпПЯL1¶ФУ¦µДєЇКэ±нґпКЅЈ»
ЈЁ2Ј©ИфТФµгAЎўCЎўPЎўQОЄ¶ҐµгµДЛД±ЯРОЗЎОЄЖЅРРЛД±ЯРОЈ¬ЗуіцµгPµДЧш±кЈ»
ЈЁ3Ј©ЙиµгRОЄЕЧОпПЯL1ЙПБнТ»ёц¶ЇµгЈ¬ЗТCAЖЅ·ЦЎПPCRЈ¬ИфOQЎОPRЈ¬ЗуіцµгQµДЧш±кЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЎ°ГїМм¶НБ¶Т»РЎК±Ј¬ЅЎїµЙъ»оТ»±ІЧУЎ±Ј¬ОЄБЛСЎ°ОЎ°Сф№вґуїОМГЎ±БмІЩФ±РЈЧйЦЇіхЦРИэёцДкј¶НЖСЎіцАґµД15ГыБмІЩФ±ЅшРР±ИИьЈ¬іЙјЁИзПВ±нЈє
іЙјЁ/·Ц | 7 | 8 | 9 | 10 |
ИЛКэ/ИЛ | 2 | 5 | 4 | 4 |
ИфИОТвСЎФсТ»ГыБмІЩФ±µДїЙДЬРФПаН¬
ЈЁ1Ј©ИОТвСЎИЎТ»ГыБмІЩФ±Ј¬СЎµЅіЙјЁЧоµНБмІЩФ±µДёЕВККЗ_________Ј®
ЈЁ2Ј©ТСЦЄ»сµГ10·ЦµДСЎКЦЦРЈ¬ЖЯЎў°ЛЎўѕЕДкј¶·Ц±рУР1ИЛЈ¬2ИЛЈ¬1ИЛЈ¬С§РЈЧј±ёґУЦРЛж»ъСЎИЎБЅИЛБмІЩЈ¬ЗуЗЎєГСЎµЅ°ЛДкј¶БЅГыБмІЩФ±µДёЕВКЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЄБЛБЛЅв°ај¶С§ЙъКэС§їОЗ°Ф¤П°µДѕЯМеЗйїцЈ¬ЦЈАПК¦¶Ф±ѕ°аІї·ЦС§ЙъЅшРРБЛОЄЖЪТ»ёцФВµДёъЧЩµчІйЈ¬ЛыЅ«µчІйЅб№ы·ЦОЄЛДАаЈєAЈєєЬєГЈ»BЈєЅПєГЈ»CЈєТ»°гЈ»DЈєІ»ґп±кЈ¬ІўЅ«µчІйЅб№ы»жЦЖіЙТФПВБЅ·щІ»НкХыµДНіјЖНјЈ¬ЗлДгёщѕЭНіјЖНјЅвґрПВБРОКМвЈє

ЈЁ1Ј©CАаЕ®ЙъУРЎЎ ЎЎГыЈ¬DАаДРЙъУРЎЎ ЎЎГыЈ¬Ѕ«ЙПГжМхРОНіјЖНјІ№ідНкХыЈ»
ЈЁ2Ј©ЙИРОНіјЖНјЦРЎ°їОЗ°Ф¤П°І»ґп±кЎ±¶ФУ¦µДФІРДЅЗ¶ИКэКЗЎЎ ЎЎЈ»
ЈЁ3Ј©ОЄБЛ№ІН¬ЅшІЅЈ¬ЦЈАПК¦ПлґУ±»µчІйµДAАаєНDАаС§ЙъЦРёчЛж»ъ»ъійИЎТ»О»Н¬С§ЅшРРЎ°Т»°пТ»Ў±»ҐЦъС§П°Ј¬ЗлУГ»КчЧґНј»тБР±нµД·Ѕ·ЁЗуіцЛщСЎБЅО»Н¬С§ЗЎєГКЗТ»ДРТ»Е®Н¬С§µДёЕВКЈ¬
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬Гж»эОЄ![]() µДѕШРО
µДѕШРО![]() ФЪµЪ¶юПуПЮЈ¬
ФЪµЪ¶юПуПЮЈ¬![]() Ул
Ул![]() ЦбЖЅРРЈ¬·ґ±ИАэєЇКэ
ЦбЖЅРРЈ¬·ґ±ИАэєЇКэ![]() ѕ№э
ѕ№э![]() БЅµгЈ¬Ц±ПЯ
БЅµгЈ¬Ц±ПЯ![]() ЛщФЪЦ±ПЯ
ЛщФЪЦ±ПЯ![]() Ул
Ул![]() ЦбЎў
ЦбЎў![]() ЦбЅ»УЪ
ЦбЅ»УЪ![]() БЅµгЈ¬ЗТ
БЅµгЈ¬ЗТ![]() ОЄПЯ¶О
ОЄПЯ¶О![]() µДИэµИ·ЦµгЈ¬Фт
µДИэµИ·ЦµгЈ¬Фт![]() µДЦµОЄЈЁ Ј©
µДЦµОЄЈЁ Ј©
A.![]() B.
B.![]()
C.![]() D.
D.![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
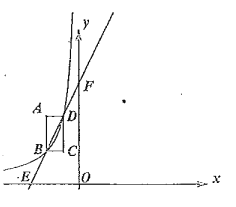
ЎѕМвДїЎїµг![]() ОЄНјРО
ОЄНјРО![]() ЙПИОТвТ»µгЈ¬№эµг
ЙПИОТвТ»µгЈ¬№эµг![]() Чч
Чч![]() Ц±ПЯ
Ц±ПЯ![]() ґ№ЧгОЄ
ґ№ЧгОЄ![]() Ј¬јЗ
Ј¬јЗ![]() µДі¤¶ИОЄ
µДі¤¶ИОЄ![]() .
.
¶ЁТеТ»:Иф![]() ґжФЪЧоґуЦµЈ¬ФтіЖЖдОЄЎ°НјРО
ґжФЪЧоґуЦµЈ¬ФтіЖЖдОЄЎ°НјРО![]() µЅЦ±ПЯ
µЅЦ±ПЯ![]() µДПЮѕаАлЎ±Ј¬јЗЧч
µДПЮѕаАлЎ±Ј¬јЗЧч![]() Ј»
Ј»
¶ЁТе¶ю:Иф![]() ґжФЪЧоРЎЦµЈ¬ФтіЖЖдОЄЎ°НјРО
ґжФЪЧоРЎЦµЈ¬ФтіЖЖдОЄЎ°НјРО![]() µЅЦ±ПЯ
µЅЦ±ПЯ![]() µД»щѕаАлЎ±Ј¬јЗЧч
µД»щѕаАлЎ±Ј¬јЗЧч![]() Ј»
Ј»
ЈЁ1Ј©ТСЦЄЦ±ПЯ![]() Ј¬ЖЅГжДЪ·ґ±ИАэєЇКэ
Ј¬ЖЅГжДЪ·ґ±ИАэєЇКэ![]() ФЪµЪТ»ПуПЮДЪµДНјПујЗЧч
ФЪµЪТ»ПуПЮДЪµДНјПујЗЧч![]() Фт
Фт![]() Ј®
Ј®
ЈЁ2Ј©ТСЦЄЦ±ПЯ![]() Ј¬µг
Ј¬µг![]() Ј¬µг
Ј¬µг![]() КЗ
КЗ![]() ЦбЙПТ»ёц¶ЇµгЈ¬
ЦбЙПТ»ёц¶ЇµгЈ¬![]() µД°лѕ¶ОЄ
µД°лѕ¶ОЄ![]() Ј¬µг
Ј¬µг![]() ФЪ
ФЪ![]() ЙПЈ¬Иф
ЙПЈ¬Иф![]() ЗуґЛК±
ЗуґЛК±![]() µДИЎЦµ·¶О§Ј¬
µДИЎЦµ·¶О§Ј¬
ЈЁ3Ј©ТСЦЄЦ±ПЯ![]() єг№э¶Ёµг
єг№э¶Ёµг![]() Ј¬µг
Ј¬µг![]() єгФЪЦ±ПЯ
єгФЪЦ±ПЯ![]() ЙПЈ¬µг
ЙПЈ¬µг![]() КЗЖЅГжЙПТ»¶ЇµгЈ¬јЗТФµг
КЗЖЅГжЙПТ»¶ЇµгЈ¬јЗТФµг![]() ОЄ¶ҐµгЈ¬ФµгОЄ¶ФЅЗПЯЅ»µгµДХэ·ЅРООЄНјРО
ОЄ¶ҐµгЈ¬ФµгОЄ¶ФЅЗПЯЅ»µгµДХэ·ЅРООЄНјРО![]()
![]() Ј¬ИфЗлЦ±ЅУРґіц
Ј¬ИфЗлЦ±ЅУРґіц![]() µДИЎЦµ·¶О§Ј®
µДИЎЦµ·¶О§Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
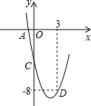
ЎѕМвДїЎї¶юґОєЇКэ![]() µДІї·ЦНјПуИзНјЛщКѕЈ¬ЖдЦРНјПуУл
µДІї·ЦНјПуИзНјЛщКѕЈ¬ЖдЦРНјПуУл![]() ЦбЅ»УЪµг
ЦбЅ»УЪµг![]() Ј¬Ул
Ј¬Ул![]() ЦбЅ»УЪµг
ЦбЅ»УЪµг![]() Ј¬ЗТѕ№эµг
Ј¬ЗТѕ№эµг![]() Ј®
Ј®
![]() ЗуґЛ¶юґОєЇКэµДЅвОцКЅЈ»
ЗуґЛ¶юґОєЇКэµДЅвОцКЅЈ»
![]() Ѕ«ґЛ¶юґОєЇКэµДЅвОцКЅРґіЙ
Ѕ«ґЛ¶юґОєЇКэµДЅвОцКЅРґіЙ![]() µДРОКЅЈ¬ІўЦ±ЅУРґіц¶ҐµгЧш±кТФј°ЛьУл
µДРОКЅЈ¬ІўЦ±ЅУРґіц¶ҐµгЧш±кТФј°ЛьУл![]() ЦбµДБнТ»ёцЅ»µг
ЦбµДБнТ»ёцЅ»µг![]() µДЧш±кЈ®
µДЧш±кЈ®
![]() АыУГТФЙПРЕПўЅвґрПВБРОКМвЈєИф№ШУЪ
АыУГТФЙПРЕПўЅвґрПВБРОКМвЈєИф№ШУЪ![]() µДТ»ФЄ¶юґО·ЅіМ
µДТ»ФЄ¶юґО·ЅіМ![]() ЈЁ
ЈЁ![]() ОЄКµКэЈ©ФЪ
ОЄКµКэЈ©ФЪ![]() µД·¶О§ДЪУРЅвЈ¬Фт
µД·¶О§ДЪУРЅвЈ¬Фт![]() µДИЎЦµ·¶О§КЗ________Ј®
µДИЎЦµ·¶О§КЗ________Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµ![]() ЦРЈ¬ЕЧОпПЯ
ЦРЈ¬ЕЧОпПЯ![]() Ул
Ул![]() ЦбЅ»УЪ
ЦбЅ»УЪ![]() БЅµг(µг
БЅµг(µг![]() ФЪµг
ФЪµг![]() µДЧуІа)Ј¬ѕ№эµг
µДЧуІа)Ј¬ѕ№эµг![]() µДЦ±ПЯ
µДЦ±ПЯ![]() Ул
Ул![]() ЦбЅ»УЪµг
ЦбЅ»УЪµг![]() УлЕЧОпПЯµДБнТ»ёцЅ»µгОЄЈ¬ЗТ
УлЕЧОпПЯµДБнТ»ёцЅ»µгОЄЈ¬ЗТ![]() Ј®
Ј®
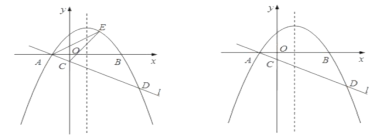
ЈЁ1Ј©Ц±ЅУРґіцµг![]() µДЧш±кЈ¬ІўЗуЦ±ПЯ
µДЧш±кЈ¬ІўЗуЦ±ПЯ![]() µДєЇКэ±нґпКЅ(ЖдЦР
µДєЇКэ±нґпКЅ(ЖдЦР![]() УГє¬
УГє¬![]() µДКЅЧУ±нКѕ)Ј»
µДКЅЧУ±нКѕ)Ј»
ЈЁ2Ј©µг![]() КЗЦ±ПЯ
КЗЦ±ПЯ![]() ЙП·ЅµДЕЧОпПЯЙПµД¶ЇµгЈ¬Иф
ЙП·ЅµДЕЧОпПЯЙПµД¶ЇµгЈ¬Иф![]() µДГж»эµДЧоґуЦµОЄ
µДГж»эµДЧоґуЦµОЄ![]() Ј¬Зу
Ј¬Зу![]() µДЦµЈ»
µДЦµЈ»
ЈЁ3Ј©Йи![]() КЗЕЧОпПЯ¶ФіЖЦбЙПµДТ»µгЈ¬µг
КЗЕЧОпПЯ¶ФіЖЦбЙПµДТ»µгЈ¬µг![]() ФЪЕЧОпПЯЙПЈ¬ТФµг
ФЪЕЧОпПЯЙПЈ¬ТФµг![]() ОЄ¶ҐµгµДЛД±ЯРОДЬ·сіЙОЄѕШРОЈїИфДЬЈ¬Зуіцµг
ОЄ¶ҐµгµДЛД±ЯРОДЬ·сіЙОЄѕШРОЈїИфДЬЈ¬Зуіцµг![]() µДЧш±кЈ»ИфІ»ДЬЈ¬ЗлЛµГчАнУЙЈ®
µДЧш±кЈ»ИфІ»ДЬЈ¬ЗлЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЎчABCЦРЈ¬ ![]() Ј¬
Ј¬ ![]() ЎгЈ¬µгDКЗПЯ¶ОBCЙПµД¶ЇµгЈ¬Ѕ«ПЯ¶ОADИЖµгAЛіК±ХлРэЧЄ50ЎгЦБ
ЎгЈ¬µгDКЗПЯ¶ОBCЙПµД¶ЇµгЈ¬Ѕ«ПЯ¶ОADИЖµгAЛіК±ХлРэЧЄ50ЎгЦБ![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() Ј®ТСЦЄAB
Ј®ТСЦЄAB![]() 2cmЈ¬ЙиBDОЄx cmЈ¬B
2cmЈ¬ЙиBDОЄx cmЈ¬B![]() ОЄy cmЈ®
ОЄy cmЈ®
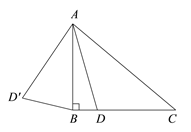
РЎГчёщѕЭС§П°єЇКэµДѕСйЈ¬¶ФєЇКэyЛжЧФ±дБїxµД±д»Ї¶ш±д»ЇµД№жВЙЅшРРБЛМЅѕїЈ¬ПВГжКЗРЎГчµДМЅѕї№эіМЈ¬ЗлІ№ідНкХыЈ®ЈЁЛµГчЈєЅвґрЦРЛщМоКэЦµѕщ±ЈБфТ»О»РЎКэЈ©
ЈЁ1Ј©НЁ№эИЎµгЎў»НјЎўІвБїЈ¬µГµЅБЛ![]() Ул
Ул![]() µДјёЧйЦµЈ¬ИзПВ±нЈє
µДјёЧйЦµЈ¬ИзПВ±нЈє
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
ЈЁ2Ј©ЅЁБўЖЅГжЦ±ЅЗЧш±кПµЈ¬ГиіцТФІ№И«єуµД±нЦРёч¶Ф¶ФУ¦ЦµОЄЧш±кµДµгЈ¬»іцёГєЇКэµДНјПуЈ®

ЈЁ3Ј©ЅбєП»іцµДєЇКэНјПуЈ¬ЅвѕцОКМвЈє
ПЯ¶О![]() µДі¤¶ИµДЧоРЎЦµФјОЄ__________
µДі¤¶ИµДЧоРЎЦµФјОЄ__________ ![]() Ј»
Ј»
Иф![]()
![]() Ј¬Фт
Ј¬Фт![]() µДі¤¶ИxµДИЎЦµ·¶О§КЗ_____________Ј®
µДі¤¶ИxµДИЎЦµ·¶О§КЗ_____________Ј®
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com