
【题目】在平面直角坐标系中,O为坐标原点,点A(-a,a)(a>0),点B(-a-4,a+3),C为该直角坐标系内的一点,连结AB,OC.若AB∥OC且AB=OC,则点C的坐标为________
【答案】(-4,3),(4,-3)
【解析】
根据题意画出图形,由AB∥OC,AB=OC,易证△ABD≌△OCE≌△OFC, 可得出BD=CE,AD=OE,再根据点A、B的坐标求出AD、BD的长,根据点C的位置(在第二象限和第四象限),写出点C的坐标,即可求解.
如图
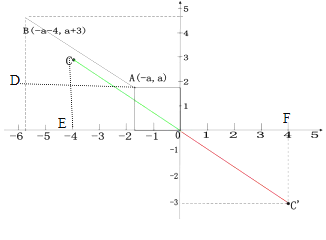
∵AB∥OC,AB=OC
易证△ABD≌△OCE≌△OFC
∴BD=CE,AD=OE
∵点A(-a,a)(a>0),点B(-a-4,a+3)
∴AD=-a-(-a-4)=4,BD=a+3-a=3
∴OE=4,CE=3
∵点C在第二象限,
∴点C的坐标为(-4,3)
∵点C和点C关于原点对称
∴C的坐标为(4,-3)
故答案为:(-4,3),(4,-3).


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣5(a≠0)经过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.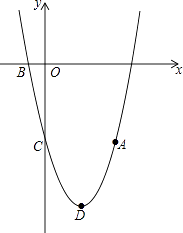
(1)求这条抛物线的表达式;
(2)连结AB、BC、CD、DA,求四边形ABCD的面积;
(3)如果点E在y轴的正半轴上,且∠BEO=∠ABC,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=30°,BC=2 ![]() ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( ) 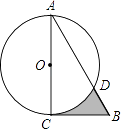
A.![]() ﹣
﹣ ![]()
B.![]() ﹣
﹣ ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点M的坐标为(3,﹣2),线段AB的位置如图所示,其中点A的坐标为(7,3),点B的坐标为(1,4).
(1)将线段AB平移可以得到线段MN,其中点A的对应点为M(3,﹣2),点B的对应点为N,则点N的坐标为 .
(2)在(1)的条件下,若点C的坐标为(4,0),请在图中描出点N并顺次连接BC,CM,MN,NB,然后求出四边形BCMN的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一单杆高2.2m,两立柱之间的距离为1.6m,将一根绳子的两端栓于立柱与铁杠结合处,绳子自然下垂呈抛物线状. 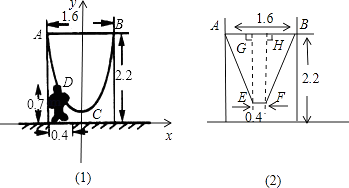
(1)一身高0.7m的小孩站在离立柱0.4m处,其头部刚好触上绳子,求绳子最低点到地面的距离;
(2)为供孩子们打秋千,把绳子剪断后,中间系上一块长为0.4米的木板,除掉系木板用去的绳子后,两边的绳子正好各为2米,木板与地面平行,求这时木板到地面的距离.(供选用数据: ![]() ≈1.8,
≈1.8, ![]() ≈1.9,
≈1.9, ![]() ≈2.1)
≈2.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若![]() ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:
(1)试说明![]() ;
;
(2)如果大正方形的面积是10,小正方形的面积是2,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
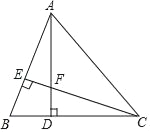
【题目】如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD≌△CFD;
(2)已知BC=7,AD=5,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com