
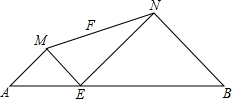
 如图,已知AB=9,点E是线段AB上的动点,分别以AE、EB为底边在线段AB的同侧作等腰直角△AME和△BNE,连接MN,设MN的中点为F,当点E从点A运动到点B时,则点F移动路径的长是$\frac{9}{2}$.
如图,已知AB=9,点E是线段AB上的动点,分别以AE、EB为底边在线段AB的同侧作等腰直角△AME和△BNE,连接MN,设MN的中点为F,当点E从点A运动到点B时,则点F移动路径的长是$\frac{9}{2}$. 分析 分别延长AM、BN交于点C,构造平行四边形MENC,根据平行四边形的性质,即可得到F为CE中点,根据F的运行轨迹为△CAB的中位线,点F移动路径的长等于AB的一半,即可得到点F移动路径的长.
解答 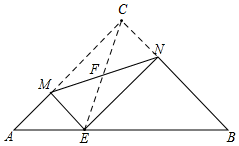 解:如图,分别延长AM、BN交于点C,
解:如图,分别延长AM、BN交于点C,
∵∠A=∠BEN=45°,
∴AC∥EN,
同理可得,BC∥EM,
∴四边形MENC为平行四边形,
∴CE与MN互相平分,
∵F为MN的中点,
∴F为CE中点,
当点E从点A运动到点B时,F始终为CE的中点,
故F的运行轨迹为△CAB的中位线,点F移动路径的长等于AB的一半,
∴F的移动路径长为$\frac{1}{2}$×9=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查了三角形中位线定理及等腰直角三角形的性质,解答本题的关键是作出辅助线,找到点F移动的轨迹.


科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2012个点的横坐标为( )
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2012个点的横坐标为( )| A. | 40 | B. | 45 | C. | 50 | D. | 55 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com