
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
分析 根据三个互不相等的有理数,既表示为1,a+b,a的形式,又可以表示为0,b,$\frac{b}{a}$的形式,也就是说这两个数组的数分别对应相等,即a+b与a中有一个是0,与b中有一个是1,再根据分式有意义的条件判断出a、b的值,代入计算即可.
解答 解:∵三个互不相等的有理数,既表示为1,a+b,a的形式,又可以表示为0,$\frac{b}{a}$,b的形式,
∴这两个数组的数分别对应相等.
∴a+b与a中有一个是0,$\frac{b}{a}$与b中有一个是1,但若a=0,会使$\frac{b}{a}$无意义,
∴a≠0,只能a+b=0,即a=-b,于是$\frac{b}{a}$=-1.只能是b=1,于是a=-1;
则a2017+b2018=(-1)2017+12018=-1+1=0,
故选:A.
点评 本题考查的是有理数的概念,能根据题意得出“a+b与a中有一个是0,$\frac{b}{a}$与b中有一个是1”是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
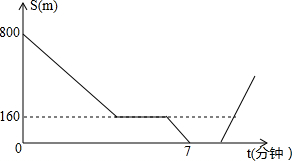 在一次集训中,一支队伍出发20分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后维续按原速原路返回,在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象,若传达命令所花时间都为2分钟.则当通讯员再次回到队尾时.他一共走了$\frac{3880}{3}$米.
在一次集训中,一支队伍出发20分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后维续按原速原路返回,在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象,若传达命令所花时间都为2分钟.则当通讯员再次回到队尾时.他一共走了$\frac{3880}{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
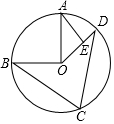 如图,点A,B,C,D是⊙O上顺次4点,OA⊥OB,AE⊥OD于E,当∠C=70°时,∠A的度数是( )
如图,点A,B,C,D是⊙O上顺次4点,OA⊥OB,AE⊥OD于E,当∠C=70°时,∠A的度数是( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com