
【题目】如图1,在平面直角坐标系中,A(a,b),B(c,0)是x轴正半轴上一点,∠ABO=30°,若![]() 与|2﹣a|互为相反数.
与|2﹣a|互为相反数.

(1)求c的值;
(2)如图2,AC⊥AB交x轴于C,以AC为边的正方形ACDE的对角线AD交x轴于F.
①求证:BE=2OC;
②记BF2﹣OF2=m,OC2=n,求![]() 的值.
的值.
【答案】(1)2+2![]() ;(2)①详见解析;②3.
;(2)①详见解析;②3.
【解析】
(1)利用非负数的性质求出a,b的值,可得点A的坐标,如图1中,过点A作AH⊥OB于H.解直角三角形求出OH,BH即可解决问题.
(2)①如图2中,延长AC交y轴于G,过点A作AT⊥OA交OB于T.证△AOG≌△ATB(AAS),推出AG=AB,∠AGO=∠ABT=30°可得结论.
②如图2中,连接GF.证明△GAF≌△BAF(SAS),推出BF=FG可得结论.
(1)解:∵![]() 与|2﹣a|互为相反数,
与|2﹣a|互为相反数,
又∵![]() ≥0,|2﹣a|≥0,
≥0,|2﹣a|≥0,
∴a=b=2,
∴A(2,2),
如图1中,过点A作AH⊥OB于H.
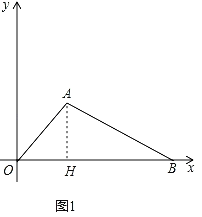
∴AH=OH=2,
在Rt△AHB中,∵∠AHB=90°,AH=2,∠ABH=30°,
∴tan∠ABH=![]() =tan30°
=tan30°
∴ BH=![]() AH=2
AH=2![]() ,
,
∴OB=2+2![]() ,
,
∴B(2+2![]() ,0).
,0).
(2)①证明:如图2中,延长AC交y轴于G,过点A作AT⊥OA交OB于T.

由(1)可知∠AOB=45°,
∵OA⊥AT,AC⊥AB,
∴∠OAT=∠CAB=90°,
∴∠OAG=∠TAB,∠ATO=∠AOT=45°,
∴OA=OT,
∵∠AOG=∠ATB=135°,
∴△AOG≌△ATB(AAS),
∴AG=AB,∠AGO=∠ABT=30°,
∵四边形ACDE是正方形,
∴AC=AE,
∵AG=AB,
∴CG=BE,
∵∠COG=90°∠CGO=30°,
∴CG=2OC,
∴BE=2OC.
②解:如图2中,连接GF.
∵AG=AB,∠GAF=∠BAF=45°,AF=AF,
∴△GAF≌△BAF(SAS),
∴BF=FG,
∴m=BF2﹣OF2=GF2﹣OF2=OG2,
∵OG=![]() OC,
OC,
∴![]() =
=![]() =(
=(![]() )2=3.
)2=3.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同.
(1)求这种笔和本子的单价;
(2)该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
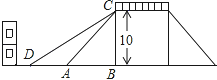
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=![]() :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结 合.研究数轴我们发现了许多重要的规律:若数轴上点 A、点 B 表示的数分别为 a、b,则A、B 两点之间的距离 AB= ![]() ,线段 AB 的中点表示的数为
,线段 AB 的中点表示的数为![]() .
.
【问题情境】如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点 A 出发, 以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒 2个单 位长度的速度向左匀速运动,设运动时间为t秒(t>0).
【综合运用】(1) 填空:
①A、B两点之间的距离AB=__________,线段AB的中点表示的数为_______;
②用含t的代数式表示:t秒后,点P表示的数为_______;点Q表示的数为_____.
(2) 求当t为何值时,P、Q 两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点 P在运动过程中,线段MN的长度是否发 生变化?若变化,请说明理由;若不变,请求出线段MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读第①小题的计算方法,再计算第②小题.
①–5![]() +(–9
+(–9![]() )+17
)+17![]() +(–3
+(–3![]() )
)
解:原式=[(–5)+(–![]() )]+[(–9)+(–
)]+[(–9)+(–![]() )]+(17+
)]+(17+![]() )+[(–3+(–
)+[(–3+(–![]() )]
)]
=[(–5)+(–9)+(–3)+17]+[(–![]() )+(–
)+(–![]() )+(–
)+(–![]() )+
)+![]() ]
]
=0+(–1![]() )
)
=–1![]() .
.
上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(﹣2000![]() )+(﹣1999
)+(﹣1999![]() )+4000
)+4000![]() +(﹣1
+(﹣1![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 的顶点为A.
的顶点为A.
(1)求点A的坐标;

(2)将线段![]() 沿
沿![]() 轴向右平移2个单位得到线段
轴向右平移2个单位得到线段![]() .
.
①直接写出点![]() 和
和![]() 的坐标;
的坐标;
②若抛物线![]() 与四边形
与四边形![]() 有且只有两个公共点,结合函数的图象,求
有且只有两个公共点,结合函数的图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约能源,某城市开展了节约水电活动,已知该城市共有10000户家庭,活动前,某调查小组随机抽取了部分家庭每月的水电费的开支(单位:元),结果如左图所示频数直方图(每一组含前一个边界值,不含后一个边界值);活动后,再次调查这些家庭每月的水电费的开支,结果如表所示:

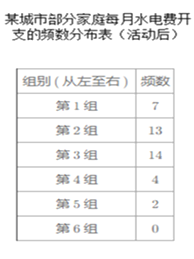
(1)求所抽取的样本的容量;
(2)如以每月水电费开支在225元以下(不含)为达到节约标准,请问通过本次活动,该城市大约增加了多少户家庭达到节约标准?
(3)活动后,这些样本家庭每月水电费开支的总额能否低于6000元?
(4)请选择一个适当的统计量分析活动前后的相关数据,并评价节约水电活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )

A. 1 B. ![]() ﹣1 C.
﹣1 C. ![]() D. 2﹣
D. 2﹣![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com