
ЁОЬтФПЁПЕфЕфЭЌбЇбЇЭъЭГМЦжЊЪЖКѓЃЌЫцЛњЕїВщСЫЫ§МвЫљдкЯНЧјШєИЩУћОгУёЕФФъСфЃЌНЋЕїВщЪ§ОнЛцжЦГЩШчЯТЩШаЮКЭЬѕаЮЭГМЦЭМЃК
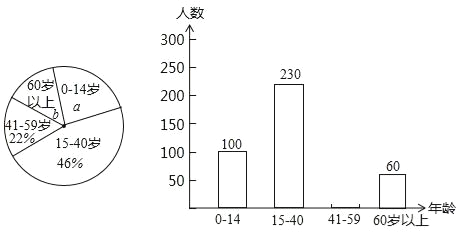
ЧыИљОнвдЩЯВЛЭъећЕФЭГМЦЭМЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЩШаЮЭГМЦЭМжаa=ЁЁ ЁЁЃЌb=ЁЁ ЁЁЃЛВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉШєИУЯНЧјЙВгаОгУё3500ШЫЃЌЧыЙРМЦФъСфдк0ЁЋ14ЫъЕФОгУёЕФШЫЪ§ЃЎ
ЃЈ3ЃЉвЛЬьЃЌЕфЕфжЊЕРСЫЯНЧјФк60ЫъвдЩЯЕФВПЗжРЯШЫВЮМгСЫЪаМЖУХЧђБШШќЃЌБШШќЕФРЯШЫУЧЗжГЩМзЁЂввСНзщЃЌЕфЕфКмЯыжЊЕРМзввСНзщЕФБШШќНсЙћЃЌЭѕДѓвЏИцЫпЫЕЃЌМззщгыввзщЕФЕУЗжКЭЮЊ110ЃЌМззщЕУЗжВЛЕЭгкввзщЕУЗжЕФ1.5БЖЃЌМззщЕУЗжзюЩйЮЊЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉ20%ЃЌ12%ЃЛЃЈ2ЃЉ700ШЫЃЛЃЈ3ЃЉМззщзюЩйЕУ66ЗжЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЁА15ЁЋ40ЁБЕФАйЗжБШКЭЦЕЪ§ПЩЧѓзмЪ§ЃЌНјЖјЧѓГіbКЭaЕФжЕЃЎРћгУзмЪ§КЭАйЗжБШЧѓГіЦЕЪ§дйВЙШЋЬѕаЮЭМЃЛ
ЃЈ2ЃЉгУбљБОЙРМЦзмЬхМДПЩЃЛ
ЃЈ3ЃЉЪзЯШЩшМззщЕУxЗжЃЌдђввзщЕУЃЈ110ЉxЃЉЗжЃЌгЩЬтвтЕУВЛЕШЙиЯЕЃКМззщЕУxЗжЁнввзщЕУxЗжЁС1.5ЃЌИљОнВЛЕШЙиЯЕСаГіВЛЕШЪНЃЌНтВЛЕШЪНМДПЩЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉзмШЫЪ§ЃК230ЁТ46%=500ЃЈШЫЃЉЃЌ100ЁТ500ЁС100%=20%ЃЌ60ЁТ500ЁС100%=12%ЃЛ
ЁЁ500ЁС22%=110ЃЈШЫЃЉЃЌШчЭМЫљЪОЃК
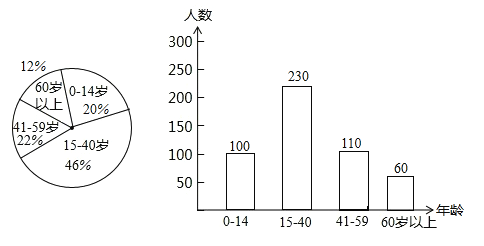
ЃЈ2ЃЉ3500ЁС20%=700ЃЈШЫЃЉЃЛ
ЃЈ3ЃЉЩшМззщЕУxЗжЃЌдђввзщЕУЃЈ110ЉxЃЉЗжЃЌгЩЬтвтЕУЃК
xЁн1.5ЃЈ110ЉxЃЉЃЌНтЕУЃКxЁн66ЃЎ
Д№ЃКМззщзюЩйЕУ66ЗжЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛжЛМзГцдк5ЁС5ЕФЗНИёЃЈУПаЁИёБпГЄЮЊ1ЃЉЩЯбизХЭјИёЯпдЫЖЏЃЌЫќДгAДІГіЗЂШЅПДЭћBЁЂCЁЂDДІЕФЦфЫќМзГцЃЌЙцЖЈЃКЯђЩЯЯђгвзпЮЊе§ЃЌЯђЯТЯђзѓзпЮЊИКЃЎР§ШчДгAЕНBМЧЮЊЃКA ЁњBЃЈ+1ЃЌ+3ЃЉЃЌДгBЕНAМЧЮЊЃКBЁњAЃЈЉ1ЃЌ-3ЃЉЃЌЦфжаЕквЛИіЪ§БэЪОзѓгвЗНЯђЃЌЕкЖўИіЪ§БэЪОЩЯЯТЗНЯђЃЎ


ЃЈ1ЃЉЭМжаA ЁњCЃЈ______ЃЌ______ЃЉЃЌB ЁњCЃЈ______ЃЌ______ЃЉЃЌCЁњ_______ЃЈ+1ЃЌЉ2ЃЉЃЛ
ЃЈ2ЃЉШєетжЛМзГцЕФаазпТЗЯпЮЊAЁњBЁњCЁњDЃЌЧыМЦЫуИУМзГцзпЙ§ЕФТЗГЬЃЛ
ЃЈ3ЃЉДгAДІШЅPДІЕФаазпТЗЯпвРДЮЮЊЃЈ+2ЃЌ+2ЃЉЃЌЃЈ+2ЃЌЉ1ЃЉЃЌЃЈЉ2ЃЌ+3ЃЉЃЌЃЈЉ1ЃЌЉ2ЃЉЃЌЧыдкЭМжаБъГіPЕФЮЛжУЃЛ
ЃЈ4ЃЉШєЭМжаСэгаСНИіИёЕуMЁЂNЃЌЧвMЁњAЃЈ3-aЃЌb-4ЃЉЃЌMЁњNЃЈ5-aЃЌb-2ЃЉЃЌдђNЁњAгІМЧЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЁїABCжаЃЌBOЁЂCOЪЧНЧЦНЗжЯпЃЎ
ЃЈ1ЃЉЁЯABC=50ЁуЃЌЁЯACB=60ЁуЃЌЧѓЁЯBOCЕФЖШЪ§ЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ2ЃЉЬтЃЈ1ЃЉжаЃЌШчНЋЁАЁЯABC=50ЁуЃЌЁЯACB=60ЁуЁБИФЮЊЁАЁЯA=70ЁуЁБЃЌЧѓЁЯBOCЕФЖШЪ§ЃЎ
ЃЈ3ЃЉШєЁЯA=nЁуЃЌЧѓЁЯBOCЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗНЗНЭЌбЇдкКЎМйЩчЛсЕїВщЪЕМљЛюЖЏжаЃЌЖдФГЙоЭЗМгЙЄГЇНјааВЩЗУЃЌЛёЕУСЫИУГЇШЅФъЕФВПЗжЩњВњаХЯЂШчЯТЃК
ЂйИУГЇвЛдТЗнЙоЭЗМгЙЄСПЮЊaЖжЃЛ
ЂкИУГЇШ§дТЗнЕФМгЙЄСПБШвЛдТЗндіГЄСЫ44ЃЅЃЛ
ЂлИУГЇЕквЛМОЖШЙВМгЙЄЙоЭЗ182ЖжЃЛ
ЂмИУГЇЖўдТЁЂШ§дТМгЙЄСПУПдТАДЯрЭЌЕФАйЗжТЪдіГЄЃЛ
ЂнИУГЇДгЫФдТЗнПЊЪМЩшБИећаоИќаТЃЌМгЙЄСПУПдТАДЯрЭЌЕФАйЗжТЪПЊЪМЯТНЕЃЛ
ЂоСљдТЗнЩшБИећаоИќаТЭъБЯЃЌДЫдТМгЙЄСПЮЊвЛдТЗнЕФ2.1БЖЃЌгыЮхдТЗнЯрБШдіГЄСЫ46.68ЖжЃЎ
РћгУвдЩЯаХЯЂЧѓЃК
ЃЈ1ЃЉИУГЇЕквЛМОЖШМгЙЄСПЕФдТЦНОљдіГЄТЪЃЛ
ЃЈ2ЃЉИУГЇвЛдТЗнЕФМгЙЄСПaЕФжЕЃЛ
ЃЈ3ЃЉИУГЇЕкЖўМОЖШЕФзмМгЙЄСПЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫТњзуЪаГЁашЧѓЃЌФГГЇМвЩњВњAЁЂBСНжжПюЪНЕФЛЗБЃЙКЮяДќЃЌУПЬьЙВЩњВњ5000ИіЃЌСНжжЙКЮяДќЕФГЩБОКЭЪлМлШчЯТБэЃК
ГЩБОЃЈдЊ/ИіЃЉ | ЪлМл ЃЈдЊ/ИіЃЉ | |
| 2 | 2.4 |
| 3 | 3.6 |
ЩшУПЬьЩњВњAжжЙКЮяДќxИіЃЌУПЬьЙВЛёРћyдЊ.
ЃЈ1ЃЉЧѓyгыxЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉШчЙћИУГЇУПЬьзюЖрЭЖШыГЩБО12000дЊЃЌФЧУДУПЬьзюЖрЛёРћЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃК
НтД№ЁАвбжЊxЉy=2ЃЌЧвxЃО1ЃЌyЃМ0ЃЌЪдШЗЖЈx+yЕФШЁжЕЗЖЮЇЁБгаШчЯТНтЗЈ
НтЃКЁпxЉy=2ЃЌЁрx=y+2 гжЁпxЃО1Ёрy+2ЃО1ЁрyЃОЉ1
гжЁпyЃМ0ЁрЉ1ЃМyЃМ0ЁЂй
ЭЌРэПЩЕУ1ЃМxЃМ2ЁЂк
гЩЂй+ЂкЕУЃКЉ1+1ЃМx+yЃМ0+2Ёрx+yЕФШЁжЕЗЖЮЇЪЧ0ЃМx+yЃМ2
АДееЩЯЪіЗНЗЈЃЌЭъГЩЯТСаЮЪЬтЃК
ЃЈ1ЃЉвбжЊxЉy=3ЃЌЧвxЃО2ЃЌyЃМ1ЃЌдђx+yЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁ
ЃЈ2ЃЉвбжЊЙигкxЃЌyЕФЗНГЬзщ![]() ЕФНтЖМЪЧе§Ъ§
ЕФНтЖМЪЧе§Ъ§
ЂйЧѓaЕФШЁжЕЗЖЮЇЃЛЂкШєaЉb=4ЃЌЧѓa+bЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCЃЌвдACЮЊЕзБпзїЕШбќЁїACDЃЌЧвЪЙЁЯABC=2ЁЯCADЃЌСЌНгBDЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌШєЁЯADC=90ЁуЃЌЁЯBAC=30ЁуЃЌBC=1ЃЌЧѓCDЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌШєЁЯADC=90ЁуЃЌжЄУїЃКAB+BC=![]() BDЃЛ
BDЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєЁЯADC=60ЁуЃЌЬНОПABЃЌBCЃЌBDжЎМфЕФЪ§СПЙиЯЕВЂжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЖдгкШЮвтСНЕуAЃЈx1ЃЌy1ЃЉB ЃЈx2ЃЌy2ЃЉЃЌЙцЖЈдЫЫуЃК
ЃЈ1ЃЉAЈB=ЃЈx1+x2ЃЌy1+y2ЃЉЃЛ
ЃЈ2ЃЉAЁбB=x1x2+y1y2ЃЛ
ЃЈ3ЃЉЕБx1=x2Чвy1=y2ЪБЃЌA=BЃЎ
гаЯТСаЫФИіУќЬтЃК
ЂйШєгаAЃЈ1ЃЌ2ЃЉЃЌBЃЈ2ЃЌЉ1ЃЉЃЌдђAЈB=ЃЈ3ЃЌ1ЃЉЃЌAЁбB=0ЃЛ
ЂкШєгаAЈB=BЈCЃЌдђA=CЃЛ
ЂлШєгаAЁбB=BЁбCЃЌдђA=CЃЛ
ЂмЃЈAЈBЃЉЈC=AЈЃЈBЈCЃЉЖдШЮвтЕуAЁЂBЁЂCОљГЩСЂЃЎ
Цфжае§ШЗЕФУќЬтЮЊ______ЃЈжЛЬюађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЫЎЙћЙЋЫОЙКНј10 000kgЦЛЙћЃЌЙЋЫОЯыжЊЕРЦЛЙћЕФЫ№ЛЕТЪ,ДгЫљгаЦЛЙћжаЫцЛњГщШЁШєИЩНјааЭГМЦЃЌВПЗжНсЙћШчЯТБэЃК
ЦЛЙћзмжЪСПn(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
Ы№ЛЕЦЛЙћжЪСПm(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
ЦЛЙћЫ№ЛЕЕФЦЕТЪ (НсЙћБЃСєаЁЪ§ЕуКѓШ§ЮЛ) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
ЙРМЦетХњЦЛЙћЫ№ЛЕЕФИХТЪЮЊ_____(НсЙћБЃСєаЁЪ§ЕуКѓвЛЮЛ)ЃЌЫ№ЛЕЕФЦЛЙћдМга______kgЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com