
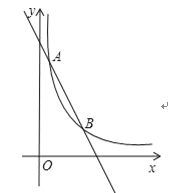
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.
(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
【答案】(1)y=-2x+8 ;(2)P(0,5) 3
【解析】试题分析:(1)将A点坐标代入反比例函数解析式即可求出m的值,再将x=3代入反比例函数解析式解得n的值,由此得出B点的坐标,结合A、B两点的坐标,利用待定系数法即可求出一次函数的表达式;
(2)作点A关于y轴的对称点A′,连接A′B交y轴于点P,在y轴上任选一点不同于P点的P′点,由三角形内两边之和大于第三边来验证点P就是我们找到的使得PA+PB的值最小的点,由A点的坐标找出点A′的坐标,由待定系数法可求出直线A′B的函数表达式,令x=0即可得出P点的坐标;再结合三角形的面积公式与点到直线的距离即可求出△PAB的面积.
试题解析:解:(1)将点A(1,6)代入反比例函数![]() 中,得6=
中,得6=![]() ,即m=6.
,即m=6.
故反比例函数的解析式为![]() .
.
∵点B(3,n)在反比例函数![]() 上,∴n=
上,∴n=![]() =2.即点B的坐标为(3,2).
=2.即点B的坐标为(3,2).
将点A(1,6)、点B(3,2)代入y=kx+b中,得: ![]() ,解得:
,解得: ![]() .
.
故一次函数的解析式为y=﹣2x+8.
(2)作点A关于y轴的对称点A′,连接A′B交y轴于点P,如图1所示.

在y轴上任取一点P′(不同于点P).∵A、A′关于y轴对称,∴AP=A′P,AP′=A′P′.在△P′A′B中,有A′P′+BP′=AP′+BP′>A′B=A′P+BP=AP+BP,∴当A′、P、B三点共线时,PA+PB最小.
∵点A的坐标为(1,6),∴点A′的坐标为(﹣1,6).
设直线A′B的解析式为y=ax+b,将点A′(﹣1,6)、点B(3,2)代入到y=ax+b中,得: ![]() ,解得:
,解得: ![]() ,∴直线A′B的解析式为y=﹣x+5,令x=0,则有y=5.
,∴直线A′B的解析式为y=﹣x+5,令x=0,则有y=5.
即点P的坐标为(0,5).
直线AB解析式为y=﹣2x+8,即2x+y﹣8=0.
AB=![]() =
=![]() ,点P到直线AB的距离d=
,点P到直线AB的距离d=![]() =
=![]() .
.
△PAB的面积S=![]() ABD=
ABD=![]() ×
×![]() ×
×![]() =3.
=3.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】(1)5(a2b-ab2)-2(ab2+3a2b);
(2)-2a+(3a-1)-(a-5);
(3)先化简,再求值:![]() x-2(x-
x-2(x-![]() y2)+(
y2)+(![]() x+
x+![]() y2),其中x=-2,y=
y2),其中x=-2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】毕节市为加快新农村建设,建设美丽乡村,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金270万元;织金县建设了2个A类村庄和5个B类村庄共投入资金1020万元.
(1)建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?
(2)黔西县改建3个A类美丽村庄和6个B类美丽村庄共需资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“元且”期间,某校组织开展“班际歌泳比赛”,甲、乙班共有学生102人(其中甲班人数多于乙班人数,且甲班人数不够100人)报名统一购买服装参加演出.下面是某服装厂给出的演出服装的价格表:
购买服装的套数 | 1~50 | 51~100 | ≥101 |
每套服装的价格/元 | 70 | 60 | 50 |
如果两班分别单独购买服装,总共要付款6580元
(1)如果甲、乙两班联合起来购买服装,那么比各自购买服装总共可以节省多少钱?
(2)甲、乙班各有多少学生报名参加比赛?
(3)如果甲班有5名学生因特殊情况不能参加演出,请你为两班设计一种省钱的购买服装方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式M=(a+b+1)x3+(2a﹣b)x2+(a+2b)x﹣4是关于x的二次多项式.
(1)若方程3(a+b)y=ky﹣8的解是y=4,求k的值;
(2)当x=2时,代数式M的值为﹣34.当x=﹣2时,求代数式M的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为□ABCD的对角线,按要求完成下列各题.

(1)用直尺和圆规作出对角线BD的垂直平分线交AD于点E,交BC于点F,垂足为O.(保留作图痕迹,不要求写作法)
(2)在(1)的基础上,连接BE和DF.求证:四边形BFDE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自我国实施“限塑令”起,开始有偿使用环保购物袋,为了满足市场需求,某厂家生产A、B两种款式的布质环保购物袋,每天生产4500个,两种购物袋的成本和售价如下表,若设每天生产A种购物袋 x个.
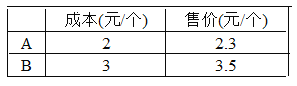
(1)用含x的整式表示每天的生产成本,并进行化简;
(2)用含x的整式表示每天获得的利润,并进行化简(利润=售价-成本);
(3)当x=1500时,求每天的生产成本与每天获得的利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
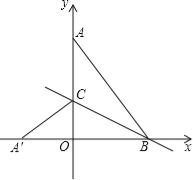
【题目】如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com