
分析 (1)每一个式子的结果等于两项的差,被减数的指数比第二个因式中第一项大1,减数都为1;
(2)根据规律得结果;
(3)将x=2代入可得结果.
解答 解:(1)(x-1)(xn+xn-1+xn-2+…+x3+x2+x+1)=xn+1-1;
故答案为:xn+1-1;
(2)当x=3时,(3-1)(32015+32014+32013+…+33+32+3+1)=32016-1;
故答案为:32016-1;
(3)当x=2时,(2-1)(22014+22013+22012+…+23+22+2+1)=22015-1,
∴22014+22013+22012+…+23+22+2+1=(22015-1)÷(2-1)=22015-1.
点评 本题考查了平方差公式、及数字类的规律题,认真阅读,总结规律,并利用规律解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AE⊥EF于点E,BF⊥EF于点F,连接AB交EF于点D.在线段AB上取一点C,使EB=EC=AC,若∠EBF=54°,则∠ABF=18°.
如图,AE⊥EF于点E,BF⊥EF于点F,连接AB交EF于点D.在线段AB上取一点C,使EB=EC=AC,若∠EBF=54°,则∠ABF=18°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
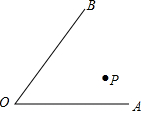 如图,∠AOB内有一点P
如图,∠AOB内有一点P查看答案和解析>>
科目:初中数学 来源: 题型:解答题
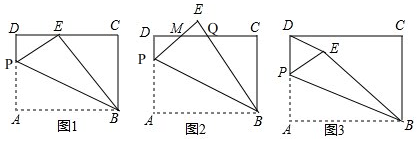
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
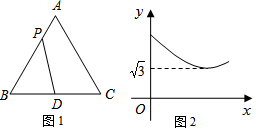 如图1,在等边△ABC中,点D是BC边的中点,点P为AB 边上的一个动点,设AP=x,PD=y,若y与x之间的函数关系的图象如图2所示,则等边△ABC的面积为( )
如图1,在等边△ABC中,点D是BC边的中点,点P为AB 边上的一个动点,设AP=x,PD=y,若y与x之间的函数关系的图象如图2所示,则等边△ABC的面积为( )| A. | 4 | B. | $2\sqrt{3}$ | C. | 12 | D. | $4\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com