
����Ŀ����ͼ1����������ABCD����࣬�������ȱ�������ADE��DCF������AF��BE��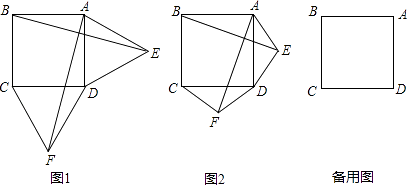
��1�����жϣ�AF��BE��������ϵ�� �� λ�ù�ϵ����
��2����ͼ2�����������������ȱ�������ADE��DCF����Ϊ����������������ADE��DCF����EA=ED=FD=FC�����ڣ�1�����еĽ����Ƿ���Ȼ�������������жϲ�����˵����
��3����������ADE��DCFΪһ�������Σ���AE=DF��ED=FC���ڣ�1�����еĽ��۶��ܳ�������ֱ��д������жϣ�
���𰸡�
��1����ȣ����ഹֱ
��2��
�⣺������Ȼ������
�����ǣ���������ABCD�У�AB=AD=CD��
���ڡ�ADE�͡�DCF�У� 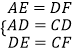 ��
��
���ADE�ա�DCF��
���DAE=��CDF��
�֡�������ABCD�У���BAD=��ADC=90�㣬
���BAE=��ADF��
���ڡ�ABE�͡�ADF�У� 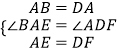 ��
��
���ABE�ա�ADF��
��BE=AF����ABM=��DAF��
�֡ߡ�DAF+��BAM=90�㣬
���ABM+��BAM=90�㣬
���ڡ�ABM�У���AMB=180�㩁����ABM+��BAM��=90�㣬
��BE��AF
��3��
�⣺�ڣ�1�����еĽ��۶��ܳ�����
�����ǣ���������ABCD�У�AB=AD=CD��
���ڡ�ADE�͡�DCF�У� 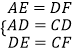 ��
��
���ADE�ա�DCF��
���DAE=��CDF��
�֡�������ABCD�У���BAD=��ADC=90�㣬
���BAE=��ADF��
���ڡ�ABE�͡�ADF�У� 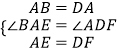 ��
��
���ABE�ա�ADF��
��BE=AF����ABM=��DAF��
�֡ߡ�DAF+��BAM=90�㣬
���ABM+��BAM=90�㣬
���ڡ�ABM�У���AMB=180�㩁����ABM+��BAM��=90�㣬
��BE��AF��
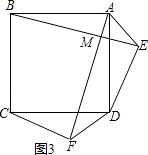
���������⣺��1��AF��BE��������ϵ�ǣ�AF=BE��λ�ù�ϵ�ǣ�AF��BE��
���ǣ���ȣ����ഹֱ��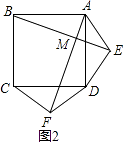
�����㾫�������ڱ��⿼��������ε��ڽǺ���Ǻ�ƽ���ı��ε����ʣ���Ҫ�˽������ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�ֲ��ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��PM2.5��ָ������ֱ��С�ڻ����2.5�Ŀ�����,�ܹ���������ķβ�Σ�����彡��.���PM2.5ָ����һ������ɿ���һ�ֹ۲ⷽ����(����)
A. ���ѡ��5����й۲�
B. ѡ��ij���½��������۲�
C. ѡ���ڴ���7���ڼ������۲�
D. ÿ���¶����ѡ��5����й۲�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ǻ����ϵ��ĸ�С����ǿ��Կ���һ������ͼ�������������˶��õ��� �� ��
A. ��ת B. ƽ�� C. ���� D. ��ת��ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�Ǿ��Σ��Ѿ�����AC�۵�����B���ڵ�E����AE��DC�Ľ���ΪO������DE�� 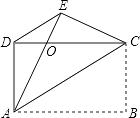
��1����֤����ADE�ա�CED��
��2����֤��DE��AC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a+b=4��c��d=��3����b+c������d��a����ֵΪ�� ��
A.7
B.��7
C.1
D.��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=12����E�ڱ�BC�ϣ�BE=EC������DCE��DE��������DFE���ӳ�EF����AB�ڵ�G������DG��BF���������½��ۣ��١�DAG�ա�DFG����BG=2AG����S��DGF=120����S��BEF= ![]() ������������ȷ���۵ĸ����ǣ� ��
������������ȷ���۵ĸ����ǣ� �� 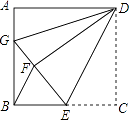
A.4
B.3
C.2
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��a��0����B��b��0������a��b����|a+2|+ ![]() =0����C������Ϊ��0��3����
=0����C��������0��3���� 
��1����a��b��ֵ��S��ABC��
��2������M��x���ϣ���S��ACM= ![]() S��ABC �� �����M�����꣮
S��ABC �� �����M�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com