
【题目】如图,![]() 为
为![]() 的内接三角形,
的内接三角形,![]() 为
为![]() 的直径,
的直径,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 为
为![]() 的切线,交
的切线,交![]() 的延长线于
的延长线于![]() .
.
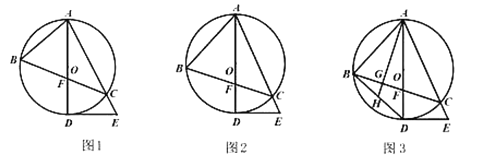
(1)求证:![]() ;
;
(2)如图,若![]() ,求证:
,求证:![]() ;
;
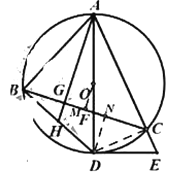
(3)如图,在(2)的条件下,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 的中点,若
的中点,若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接![]() ,根据直径所对的圆周角是直角得到
,根据直径所对的圆周角是直角得到![]() ,即
,即![]() .根据切线的性质有
.根据切线的性质有![]() ,则
,则![]() .又
.又![]() ,根据等角的余角相等即可证明.
,根据等角的余角相等即可证明.
(2)连接![]() 、
、![]() .根据
.根据![]() ,
,![]() ,得到
,得到![]() .
.
根据等边对等角得到![]() ,
,![]() 则
则![]() ,
,![]() ,
,![]() ,即
,即![]() ,即可证明.
,即可证明.
(3)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() .根据
.根据![]() ,得到
,得到![]() ,
,![]() ,则
,则![]() .又
.又![]() ,则
,则![]() . 设
. 设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,根据勾股定理,得
,根据勾股定理,得![]() ,
,![]() .又
.又![]() ,则
,则![]() ,即可求出
,即可求出![]() ,又
,又![]() ,
,![]() .易求
.易求![]() ,
,![]() ,即可求解.
,即可求解.
(1)连接![]() ,∵
,∵![]() 为直径,∴
为直径,∴![]() ,∴
,∴![]() .
.
∵![]() 为直径,
为直径,![]() 为切线,∴
为切线,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
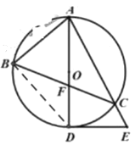
(2)连接![]() 、
、![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() .
.

(3)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() .
.
∵![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,根据勾股定理,得
,根据勾股定理,得![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,
,![]() .
.
易求![]() ,
,![]() ,∴
,∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
课题 | 测量校内旗杆高度 | ||
目的 | 运用所学数学知识及数学方法解决实际问题﹣﹣﹣测量旗杆高度 | ||
方案 | 方案一 | 方案二 | 方案三 |
示意图 |
|
| |
测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° | AM=1.5m,AB=20m ∠α=30°,∠β=60° | |
计算过程(结 果保留根号) | 解: | 解: | |
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线与x轴的两个交点及其顶点构成等边三角形,则称该抛物线“等边抛物线”.
(1)若对任意m,n,点M(m,n)和点N(-m+4,n)恒在“等边抛物线”![]() :
:![]() 上,求抛物线
上,求抛物线![]() 的解析式;
的解析式;
(2)若抛物线![]() :
:![]() “等边抛物线”,求
“等边抛物线”,求![]() 的值;
的值;
(3)对于“等边抛物线”![]() :
:![]() ,当1<x<m吋,总存在实数b。使二次函数
,当1<x<m吋,总存在实数b。使二次函数![]() 的图象在一次函数y=x图象的下方,求m的最大值.
的图象在一次函数y=x图象的下方,求m的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
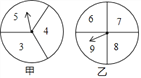
(1)请用列表的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小鲁在一个不透明的盒子里装了5个除颜色外其他都相同的小球,其中有3个是红球,2个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
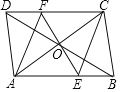
【题目】已知:四边形ABCD是平行四边形,点O是对角线AC、BD的交点,EF过点O且与AB、CD分别相交于点E、F,连接EC、AF.
(1)求证:DF=EB;(2)AF与图中哪条线段平行?请指出,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
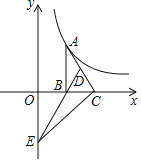
【题目】如图,已知点A在反比例函数y=![]() (x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
(x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各 300 株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性,进行了抽样调查,从甲、乙两个大棚各收集了 24 株秧苗上的小西红柿的个数,并对数据进行整理、描述和分析。
下面给出了部分信息:(说明:45 个以下为产量不合格,45 个及以上为产量合格,其中 45~65 个为产量良好,65~85 个为产量优秀)
a.补全下面乙组数据的频数分布直方图(数据分成 6 组: 25≤x<35,35≤x<45,45≤x<55,55≤x<65,65≤x<75,75≤x<85):
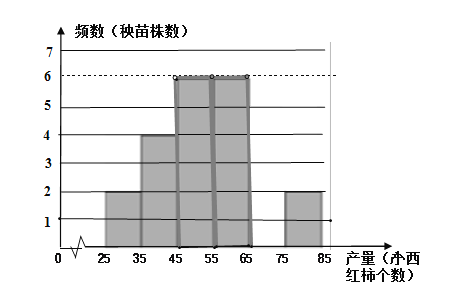
b.乙组数据在产量良好(45≤x<65)这两组的具体数据为: 46 46 47 47 48 48 55 57 57 57 58 61
c.数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 52.25 | 51 | 58 | 238 |
乙 | 52.25 | 57 | 210 |
(1)补全乙的频数分布直方图.
(2)写出表中![]() 的值.
的值.
(3)根据样本情况,估计乙大棚产量良好及以上的秧苗数为 株.
(4)根据抽样调查情况,可以推断出 大棚的小西红柿秧苗品种更适应市场需求,写出理由.(至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠1).
(k为常数,k≠1).
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com