

分析 (1)根据平行四边形的性质证明△ADP≌△CBQ,得BQ=PD,由AD=BD=BC得:BC=BD=BP+PD=BP+BQ;
(2)图②,证明△ABP≌△CDQ,得PB=DQ,根据线段的和得结论;
图③,证明△ADP≌△CBQ,得PD=BQ,同理得出结论;
(3)分别代入图①和图②条件下的BC,计算即可.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADB=∠CBD,
∵AP∥CQ,
∴∠APQ=∠CQB,
∴△ADP≌△CBQ,
∴DP=BQ,
∵AD=BD,AD=BC,
∴BD=BC,
∵BD=BP+DP,
∴BC=BP+BQ;
(2)图②:BQ-BP=BC,理由是:
∵AP∥CQ,
∴∠APB=∠CQD,
∵AB∥CD,
∴∠ABD=∠CDB,
∴∠ABP=∠CDQ,
∵AB=CD,
∴△ABP≌△CDQ,
∴BP=DQ,
∴BC=AD=BD=BQ-DQ=BQ-BP;
图③:BP-BQ=BC,理由是:
同理得:△ADP≌△CBQ,
∴PD=BQ,
∴BC=AD=BD=BP-PD=BP-BQ;
(3)图①,BC=BP+BQ=DQ+PD=1+3=4,
图②,BC=BQ-BP=PD-DQ=3-1=2,
∴BC=2或4.
点评 本题是四边形的综合题,难度适中,考查了平行四边形、全等三角形的性质和判定,动点P、Q在不同的位置,都能构建两个全等三角形,以三角形全等为突破口,得出线段相等,利用线段的和与差得出BP、BQ、BC三者之间的数量关系.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{24}$ | B. | $\sqrt{20}$ | C. | $\sqrt{\frac{3}{2}}$ | D. | $\sqrt{18}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
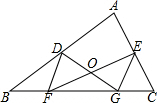 如图,在△ABC中D,E分别是AB,AC的中点,点F,G在BC上,且BC=4BF=4CG,EF与DG相交于点O,若∠DFE=40°,∠DGE=80°,那么∠DOE的度数是( )
如图,在△ABC中D,E分别是AB,AC的中点,点F,G在BC上,且BC=4BF=4CG,EF与DG相交于点O,若∠DFE=40°,∠DGE=80°,那么∠DOE的度数是( )| A. | 100° | B. | 120° | C. | 140° | D. | 160° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
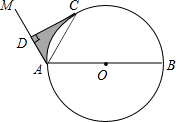 如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D.
如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形OABC为直角梯形,已知AB∥OC,BC⊥OC,A点坐标为(3,4),AB=6.
如图,四边形OABC为直角梯形,已知AB∥OC,BC⊥OC,A点坐标为(3,4),AB=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com