
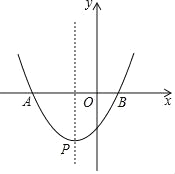
����Ŀ����ͼ��������y=ax2+bx+c��x���ཻ�ڵ�A����3��0����B��1��0������y���ཻ�ڣ�0����![]() ��������ΪP��
��������ΪP��
��1���������߽���ʽ��
��2�����������Ƿ���ڵ�E��ʹ��ABP��������ڡ�ABE������������ڣ�������������ĵ�E�����ꣻ�������ڣ���˵�����ɣ�
��3������ƽ�����Ƿ���ڵ�F��ʹ����A��B��P��FΪ������ı���Ϊƽ���ı��Σ�ֱ��д�����з��������ĵ�F�����꣬�����ƽ���ı��ε������
���𰸡���1��y=![]() x2+x��
x2+x��![]() ��2������������1��2
��2������������1��2![]() ��2����1+2
��2����1+2![]() ��2����3����F������Ϊ����1��2������3����2��������5����2������ƽ���ı��ε����Ϊ 8
��2����3����F������Ϊ����1��2������3����2��������5����2������ƽ���ı��ε����Ϊ 8
��������
��1���������߽���ʽΪy=ax2+bx+c��������3��0������1��0������0��![]() ���������a��b��c��ֵ���ɣ���2�����������߽���ʽ��֪����P�����꣬�����������εĵ���ͬ�ɵ�Ҫʹ���������������������ȣ�����P�������֪E�������꣬�������ʽ���x��ֵ���ɣ���3���ֱ�����ABΪ�ߡ�ABΪ�Խ�������������F�����겢���������ɣ�
���������a��b��c��ֵ���ɣ���2�����������߽���ʽ��֪����P�����꣬�����������εĵ���ͬ�ɵ�Ҫʹ���������������������ȣ�����P�������֪E�������꣬�������ʽ���x��ֵ���ɣ���3���ֱ�����ABΪ�ߡ�ABΪ�Խ�������������F�����겢���������ɣ�
��1���������߽���ʽΪy=ax2+bx+c��������3��0������1��0������0��![]() �����������߽���ʽ��
�����������߽���ʽ��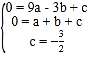 ��
��
��ã�a=![]() ��b=1��c=��
��b=1��c=��![]()
�������߽���ʽ��y=![]() x2+x��
x2+x��![]()
��2�����ڣ�
��y=![]() x2+x��
x2+x��![]() =
=![]() ��x+1��2��2
��x+1��2��2
��P����������1����2��
�ߡ�ABP��������ڡ�ABE�������
���E��AB�ľ������2��
��E��a��2����
��![]() a2+a��
a2+a��![]() =2
=2
���a1=��1��2![]() ��a2=��1+2
��a2=��1+2![]()
����������ĵ�E������Ϊ����1��2![]() ��2����1+2
��2����1+2![]() ��2��
��2��
��3���ߵ�A����3��0������B��1��0����
��AB=4
��ABΪ�ߣ�����A��B��P��FΪ������ı���Ϊƽ���ı���
��AB��PF��AB=PF=4
�ߵ�P���꣨��1����2��
���F������3����2��������5����2��
��ƽ���ı��ε����=4��2=8
��ABΪ�Խ��ߣ���A��B��P��FΪ������ı���Ϊƽ���ı���
��AB��PF����ƽ��
���F��x��y���ҵ�A����3��0������B��1��0������P����1����2��
��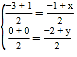 ��
��
��x=��1��y=2
���F����1��2��
��ƽ���ı��ε����=![]() ��4��4=8
��4��4=8
������������F������Ϊ����1��2������3����2��������5����2������ƽ���ı��ε����Ϊ8��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧ��ҵ�ؼ��紴ҵ����һ����ֲ�辰�뻨�ܸ�50���ۺ�ͳ�����辰��ƽ��ÿ��������160Ԫ�����ܵ�ƽ��ÿ��������19Ԫ�����з��֣�
���辰ÿ����1�����辰��ƽ��ÿ���������2Ԫ;ÿ����1�����辰��ƽ��ÿ����������2Ԫ;�ڻ��ܵ�ƽ��ÿ������ʼ�ղ���.
С���ƻ��ڶ�����ֲ�辰�뻨�ܹ�100��������ֲ���辰�ȵ�һ������x�����ڶ����辰�뻨������������ֱ�ΪW1��W2����λ��Ԫ��
��1���ú�x�Ĵ���ʽ�ֱ��ʾW1��W2;
��2����xȡ��ֵʱ���ڶ�����ֲ���辰�뻨��������õ�������W���������������Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
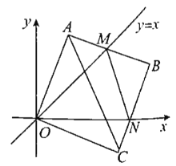
����Ŀ�����Ե�OΪԭ���ƽ��ֱ������ϵ�У��߳�Ϊ1��������OABC��������A��C�ֱ���y�ᣬ![]() ����������ϣ��ֽ�������OABC�Ƶ���˳ʱ����ת������A��һ������ֱ��
����������ϣ��ֽ�������OABC�Ƶ���˳ʱ����ת������A��һ������ֱ��![]() ��ʱ��ֹͣת������ת�����У�AB�߽�ֱ��
��ʱ��ֹͣת������ת�����У�AB�߽�ֱ��![]() �ڵ�M��BC�߽����ڵ�N��
�ڵ�M��BC�߽����ڵ�N��
��1����תֹͣʱ��������ת�Ķ�����_________.
��2������ת�����У���MN��ACƽ��ʱ��
��![]() ��
��![]() �Ƿ�ȫ�ȣ���ʱ������OABC��ת�Ķ����Ƕ��٣�
�Ƿ�ȫ�ȣ���ʱ������OABC��ת�Ķ����Ƕ��٣�
��ֱ��д��![]() ���ܳ���ֵ�����ж����ֵ��������OABC����ת�������Ƿ����仯��
���ܳ���ֵ�����ж����ֵ��������OABC����ת�������Ƿ����仯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������Ϊ�˽Ȿ���Ź��˵�������������������˳������飮�ò��������ȡ��30������ij��ÿ�˼ӹ�����ĸ������������£�
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
�����������ݣ��õ�����ͳ��ͼ��
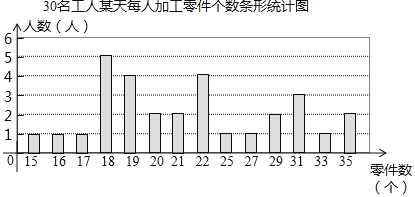
�������ݵ�ƽ��������������λ�����±���ʾ��
ͳ���� | ƽ���� | ���� | ��λ�� |
��ֵ | 23 | m | 21 |
����������Ϣ������������⣺
��1���ϱ�������m��ֵΪ�� ����
��2��Ϊ�������˵Ļ����ԣ��ò��Ÿ��ݹ���ÿ��ӹ�����ĸ����ƶ��˽����������ﵽ��������Ĺ��˽���ý������������һ�����ҵĹ����ܻ�Ӧ������ ����ȷ���������ȽϺ��ʣ�������ƽ����������������������λ������
��3���ò��Ź涨��ÿ��ӹ�����ĸ����ﵽ��25���Ĺ���Ϊ�������֣����ò�����300�����ˣ��Թ��Ƹò����������ֵ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC ��һ���Բ�����С�B=90�㣬AB��BC��������![]() ����һ�� P�� ʹ��
����һ�� P�� ʹ��![]() �����Ǽס������˵�������
�����Ǽס������˵�������
�ף���ȡ AB ���е� D���ڹ��� D ��ֱ�� AC ��ƽ���ߣ���![]() �ڵ� P����� P ��Ϊ����
�ڵ� P����� P ��Ϊ����
�ң���ȡ AC ���е� E���ڹ��� E ��ֱ��AB ��ƽ���ߣ���![]() �ڵ� P����� P ��Ϊ����
�ڵ� P����� P ��Ϊ����
���ڼס������˵������������ж���ȷ���ǣ� ��
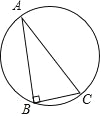
A. ���˽���ȷ B. ���˽Դ��� C. ����ȷ���Ҵ��� D. �״�������ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
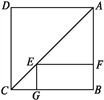
����Ŀ����ͼ,��E��������ABCD�Խ���AC��һ��,EF��AB,EG��BC,����ֱ�ΪE,F,��������ABCD���ܳ���40 cm.
(1)��֤:�ı���BFEG�Ǿ���;
(2)���ı���EFBG���ܳ�;
(3)��AF�ij�Ϊ����ʱ,�ı���BFEG��������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,��������30���ǵ���ȫ��ͬ�����ǰ�ABC��DEF��ֱ��l����,����˵���������( ��)
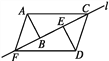
A. �ı���ACDF��ƽ���ı��� B. ����EΪBC�е�ʱ,�ı���ACDF�Ǿ���
C. ����B���E�غ�ʱ,�ı���ACDF������ D. �ı���ACDF��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
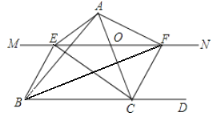
����Ŀ����ͼ����![]() �У���
����![]() ��
��![]() ����һ�����㣬����
����һ�����㣬����![]() ��ֱ��
��ֱ��![]() ����
����![]() ��
��![]() ��ƽ�����ڵ�
��ƽ�����ڵ�![]() ����
����![]() �����
�����![]() ��ƽ�����ڵ�
��ƽ�����ڵ�![]() ��
��
��1��̽��![]() ��
��![]() ��������ϵ������֤��.
��������ϵ������֤��.
��2������![]() ������
������![]() �ڱ�
�ڱ�![]() ���˶�ʱ���ı���
���˶�ʱ���ı���![]() ����Ϊ�����������ܣ���֤�����������ܣ���˵�����ɣ�
����Ϊ�����������ܣ���֤�����������ܣ���˵�����ɣ�
��3������![]() ������
������![]() ��
��![]() ���˶���ʲôλ��ʱ���ı���
���˶���ʲôλ��ʱ���ı���![]() �Ǿ��Σ���˵�����ɣ�
�Ǿ��Σ���˵�����ɣ�
��4���ڣ�3���������£�![]() ����ʲô����ʱ���ı���
����ʲô����ʱ���ı���![]() �������Σ���˵��������
�������Σ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λҪӡˢ�������������У����ؽ�ͨ��ȫ�����������ϣ���ӡˢ�������ÿ�ݲ�����1Ԫӡˢ�ѣ�����150Ԫ���ư�ѣ���ӡˢ�������ÿ�ݲ�����2.5Ԫӡˢ�ѣ������ư�ѣ�����ͬһ��ӡˢ��һ��ӡ������Ϊ![]() ��(
��(![]() ������)��
������)��
(1)�������⣬��д�±���
һ��ӡ������(��) | 5 | 10 | 20 | �� |
|
��ӡˢ���շ�(Ԫ) | 155 | �� | |||
��ӡˢ���շ�(Ԫ) | 12.5 | �� |
(2)��ӡˢƷ��������800�ݵ������ѡ�ļ�ӡˢ��ӡ��ʡǮ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com