
以等腰直角△ABC的斜边AB所在的直线为对称轴,作这个△ABC的对称图形△ ,则所得到的四边形ACBC′一定是_______.
,则所得到的四边形ACBC′一定是_______.
正方形
【解析】
试题分析:先画出图形,由题意易得,所得四边形ACBC′的四个角都是直角,又有两直角边相等,可得所得四边形是正方形.

∵△ABC是等腰直角三角形,
∴AC=BC,∠CAB=∠CBA=45°,∠C=90°,
∵△ABC和△ABC′是关于AB轴对称,
∴∠C′AB=∠C′BA=45°,∠C′=90°,
∴∠CAC′=∠CBC′=90°,
∴四边形ACBC′是矩形,
又∵AC=BC,
∴四边形ACBC′是正方形.
考点:此题主要考查等腰直角三角形的性质,轴对称的性质和正方形的判定
点评:解答本题的关键是熟练掌握三个角都是直角的四边形是矩形,有一组邻边相等的矩形是正方形.


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
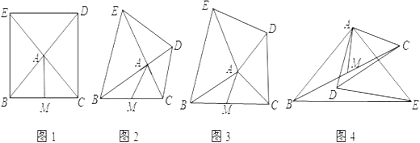
查看答案和解析>>
科目:初中数学 来源:2010年河北省唐山市中考数学一模试卷(解析版) 题型:解答题
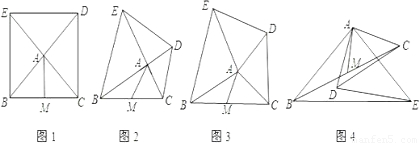
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com