
”¾ĢāÄæ”æČēĶ¼![]() £¬ČōÅ×ĪļĻß
£¬ČōÅ×ĪļĻß![]() µÄ¶„µć
µÄ¶„µć![]() ŌŚÅ×ĪļĻß
ŌŚÅ×ĪļĻß![]() ÉĻ£¬Å×ĪļĻß
ÉĻ£¬Å×ĪļĻß![]() µÄ¶„µć
µÄ¶„µć![]() Ņ²ŌŚÅ×ĪļĻß
Ņ²ŌŚÅ×ĪļĻß![]() ÉĻ£Øµć
ÉĻ£Øµć![]() Óėµć
Óėµć![]() ²»ÖŲŗĻ£©£¬ĪŅĆĒ¶ØŅå£ŗÕāŃłµÄĮ½ĢõÅ×Īļ
²»ÖŲŗĻ£©£¬ĪŅĆĒ¶ØŅå£ŗÕāŃłµÄĮ½ĢõÅ×Īļ![]() £¬
£¬![]() »„ĪŖ”°ÓŃŗĆ”±Å×ĪļĻߣ¬æɼūŅ»ĢõÅ×ĪļĻߵĔ°ÓŃŗĆ”±Å×ĪļĻßæÉŅŌÓŠ¶ąĢõ£®
»„ĪŖ”°ÓŃŗĆ”±Å×ĪļĻߣ¬æɼūŅ»ĢõÅ×ĪļĻߵĔ°ÓŃŗĆ”±Å×ĪļĻßæÉŅŌÓŠ¶ąĢõ£®
![]() ČēĶ¼
ČēĶ¼![]() £¬ŅŃÖŖÅ×ĪļĻß
£¬ŅŃÖŖÅ×ĪļĻß![]() Óė
Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £¬ŹŌĒó³öµć
£¬ŹŌĒó³öµć![]() ¹ŲÓŚøĆÅ×ĪļĻ߶Ō³ĘÖį¶Ō³ĘµÄµć
¹ŲÓŚøĆÅ×ĪļĻ߶Ō³ĘÖį¶Ō³ĘµÄµć![]() µÄ×ų±ź£»
µÄ×ų±ź£»
![]() ĒėĒó³öŅŌµć
ĒėĒó³öŅŌµć![]() ĪŖ¶„µćµÄ
ĪŖ¶„µćµÄ![]() µÄÓŃŗĆÅ×ĪļĻß
µÄÓŃŗĆÅ×ĪļĻß![]() µÄ½āĪöŹ½£¬²¢Öø³ö
µÄ½āĪöŹ½£¬²¢Öø³ö![]() Óė
Óė![]() ÖŠ
ÖŠ![]() Ķ¬Ź±Ėę
Ķ¬Ź±Ėę![]() Ōö“ó¶ųŌö“óµÄ×Ō±äĮæµÄȔֵ·¶Ī§£»
Ōö“ó¶ųŌö“óµÄ×Ō±äĮæµÄȔֵ·¶Ī§£»
![]() ČōÅ×Īļ
ČōÅ×Īļ![]() µÄČĪŅāŅ»ĢõÓŃŗĆÅ×ĪļĻߵĽāĪöŹ½ĪŖ
µÄČĪŅāŅ»ĢõÓŃŗĆÅ×ĪļĻߵĽāĪöŹ½ĪŖ![]() £¬ĒėŠ“³ö
£¬ĒėŠ“³ö![]() Óė
Óė![]() µÄ¹ŲĻµŹ½£¬²¢ĖµĆ÷ĄķÓÉ£®
µÄ¹ŲĻµŹ½£¬²¢ĖµĆ÷ĄķÓÉ£®

”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©
£»£Ø2£©![]() £¬
£¬![]() £»£Ø3£©
£»£Ø3£©![]() £®
£®
”¾½āĪö”æ
£Ø1£©Éčx=0£¬Ēó³öyµÄÖµ£¬¼“æɵƵ½CµÄ×ų±ź£¬°ŃÅ×ĪļĻßL3£ŗy=2x2©8x+4Åä·½¼“æɵƵ½Å×ĪļĻߵĶŌ³ĘÖį£¬ÓÉ“ĖæÉĒó³öµćC¹ŲÓŚøĆÅ×ĪļĻ߶Ō³ĘÖį¶Ō³ĘµÄ¶Ō³ĘµćDµÄ×ų±ź£»
£Ø2£©ÓÉ£Ø1£©æÉÖŖµćDµÄ×ų±źĪŖ£Ø4£¬4£©£¬ŌŁÓÉĢõ¼žŅŌµćDĪŖ¶„µćµÄL3µÄ”°ÓŃŗĆ”±Å×ĪļĻßL4µÄ½āĪöŹ½£¬æÉĒó³öL4µÄ½āĪöŹ½£¬½ų¶ųæÉĒó³öL3ÓėL4ÖŠyĶ¬Ź±ĖęxŌö“ó¶ųŌö“óµÄ×Ō±äĮæµÄȔֵ·¶Ī§£»
£Ø3£©øł¾ŻÅ×ĪļĻßL1µÄ¶„µćAŌŚÅ×ĪļĻßL2ÉĻ£¬Å×ĪļĻßL2µÄ¶„µćBŅ²ŌŚÅ×ĪļĻßL1ÉĻ£¬æÉŅŌĮŠ³öĮ½øö·½³Ģ£¬Ļą¼ÓæÉµĆ£Øa1+a2£©£Øh©m£©2=0£®æɵĆa1+a2=0£®
£Ø1£©”ßÅ×ĪļĻßL3£ŗy=2x2©8x+4£¬”ąy=2£Øx©2£©2©4£¬”ą¶„µćĪŖ£Ø2£¬£4£©£¬¶Ō³ĘÖįĪŖx=2£¬Éčx=0£¬Ōņy=4£¬”ąC£Ø0£¬4£©£¬”ąµćC¹ŲÓŚøĆÅ×ĪļĻ߶Ō³ĘÖį¶Ō³ĘµÄ¶Ō³ĘµćDµÄ×ų±źĪŖ£ŗ£Ø4£¬4£©£»
£Ø2£©”ßŅŌµćD£Ø4£¬4£©ĪŖ¶„µćµÄL3µÄÓŃŗĆÅ×ĪļĻßL4»¹¹żµć£Ø2£¬©4£©£¬”ąL4µÄ½āĪöŹ½ĪŖy=©2£Øx©4£©2+4£¬ÓÉĶ¼ĻóæÉÖŖ£¬µ±2”Üx”Ü4Ź±£¬Å×ĪļĻßL3ÓėL4ÖŠyĶ¬Ź±ĖęxŌö“ó¶ųŌö“ó£»
£Ø3£©a1Óėa2µÄ¹ŲĻµŹ½ĪŖa1+a2=0£®
ĄķÓÉČēĻĀ£ŗ
”ßÅ×ĪļĻßy=a1 £Øx©m£©2+nµÄŅ»Ģõ”°ÓŃŗĆ”±Å×ĪļĻߵĽāĪöŹ½ĪŖy=a2 £Øx©h£©2+k£¬”ąy=a2 £Øx©h£©2+k¹żµć£Øm£¬n£©£¬ĒŅy=a1 £Øx©m£©2+n¹żµć£Øh£¬k£©£¬¼“
k=a1 £Øh©m£©2+n”¢Ł
n=a2 £Øm©h£©2+k”¢Ś
ÓÉ¢Ł+¢ŚµĆ£ŗ£Øa1+a2£©£Øh©m£©2=0£®
ÓÖ”°ÓŃŗĆ”±Å×ĪļĻߵĶ„µć²»ÖŲŗĻ£¬”ąh”Łm£¬”ąa1+a2=0£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬½«Ö±½ĒČż½ĒŠĪ·Öøī³ÉŅ»øöÕż·½ŠĪŗĶĮ½¶ŌČ«µČµÄÖ±½ĒČż½ĒŠĪ£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £»ŌŚÕż·½ŠĪ
£»ŌŚÕż·½ŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() .
.

Ģ½¾æ1
£Ø1£©Š”Ć÷·¢ĻÖĮĖĒóÕż·½ŠĪ±ß³¤µÄ·½·Ø£ŗÓÉĢāŅāæɵĆ![]() £¬
£¬![]() £¬ŅņĪŖ
£¬ŅņĪŖ![]() £¬ĖłŅŌ
£¬ĖłŅŌ![]() £¬½āµĆ
£¬½āµĆ![]()
Ģ½¾æ2
£Ø2£©Š”ĮĮ·¢ĻÖĮĖĮķŅ»ÖÖĒóÕż·½ŠĪ±ß³¤µÄ·½·Ø£ŗĮ¬½Ó![]() £¬ĄūÓĆ
£¬ĄūÓĆ![]() æÉŅŌµĆµ½
æÉŅŌµĆµ½![]() Óė
Óė![]() µÄ¹ŲĻµ.Ēėøł¾ŻŠ”ĮĮµÄĖ¼Ā·Ķź³ÉĖūµÄĒó½ā¹ż³Ģ.
µÄ¹ŲĻµ.Ēėøł¾ŻŠ”ĮĮµÄĖ¼Ā·Ķź³ÉĖūµÄĒó½ā¹ż³Ģ.
Ģ½¾æ3
£Ø3£©Ēė½įŗĻŠ”Ć÷ŗĶŠ”ĮĮµĆµ½µÄ½įĀŪŃéÖ¤¹“¹É¶ØĄķ.£Ø×¢£ŗøł¾Ż±ČĄżµÄ»ł±¾ŠŌÖŹ£¬ÓÉ![]() æɵĆ
æɵĆ![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy=©x+1ÓėxÖį£¬yÖį·Ö±š½»ÓŚB£¬AĮ½µć£¬¶ÆµćPŌŚĻ߶ĪABÉĻŅĘ¶Æ£¬ŅŌPĪŖ¶„µć×÷”ĻOPQ=45”ć½»xÖįÓŚµćQ£®

£Ø1£©ĒóµćAŗĶµćBµÄ×ų±ź£»
£Ø2£©±Č½Ļ”ĻAOPÓė”ĻBPQµÄ“󊔣¬ĖµĆ÷ĄķÓÉ£®
£Ø3£©ŹĒ·ń“ęŌŚµćP£¬Ź¹µĆ”÷OPQŹĒµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėĒó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©ČēĶ¼£¬![]() £¬
£¬![]() .µć
.µć![]() ŌŚÉäĻß
ŌŚÉäĻß![]() ÉĻ£¬ĄūÓĆĶ¼£¬»Ķ¼ĖµĆ÷ĆüĢā”°ÓŠĮ½±ßŗĶĘäÖŠŅ»±ßµÄ¶Ō½Ē·Ö±šĻąµČµÄĮ½øöČż½ĒŠĪČ«µČ”±ŹĒ¼ŁĆüĢā.Äć»Ķ¼Ź±£¬Ń”Č”µÄ
ÉĻ£¬ĄūÓĆĶ¼£¬»Ķ¼ĖµĆ÷ĆüĢā”°ÓŠĮ½±ßŗĶĘäÖŠŅ»±ßµÄ¶Ō½Ē·Ö±šĻąµČµÄĮ½øöČż½ĒŠĪČ«µČ”±ŹĒ¼ŁĆüĢā.Äć»Ķ¼Ź±£¬Ń”Č”µÄ![]() µÄ³¤Ō¼ĪŖ__________
µÄ³¤Ō¼ĪŖ__________![]() £Ø¾«Č·µ½0.1
£Ø¾«Č·µ½0.1![]() £©.
£©.
£Ø2£©![]() ĪŖČń½Ē£¬
ĪŖČń½Ē£¬![]() £¬µć
£¬µć![]() ŌŚÉäĻß
ŌŚÉäĻß![]() ÉĻ£¬µć
ÉĻ£¬µć![]() µ½ÉäĻß
µ½ÉäĻß![]() µÄ¾ąĄėĪŖ
µÄ¾ąĄėĪŖ![]() £¬
£¬![]() £¬Čō
£¬Čō![]() µÄŠĪד”¢“󊔏ĒĪØŅ»Č·¶ØµÄ£¬Ōņ
µÄŠĪד”¢“󊔏ĒĪØŅ»Č·¶ØµÄ£¬Ōņ![]() µÄȔֵ·¶Ī§ŹĒ__________.
µÄȔֵ·¶Ī§ŹĒ__________.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”泤³ĒæĘ¼¼¹«Ė¾Éś²śĻśŹŪŅ»ÖÖµē×Ó²śĘ·£¬øĆ²śĘ·×ܳɱ¾°üĄØ¼¼Źõ³É±¾”¢ÖĘŌģ³É±¾”¢ĻśŹŪ³É±¾Čż²æ·Ö£¬¾ŗĖĖć£¬![]() ÄźøĆ²śĘ·ø÷²æ·Ö³É±¾ĖłÕ¼±ČĄżŌ¼ĪŖ
ÄźøĆ²śĘ·ø÷²æ·Ö³É±¾ĖłÕ¼±ČĄżŌ¼ĪŖ![]() £®ĒŅ
£®ĒŅ![]() ÄźøĆ²śĘ·µÄ¼¼Źõ³É±¾”¢ÖĘŌģ³É±¾·Ö±šĪŖ
ÄźøĆ²śĘ·µÄ¼¼Źõ³É±¾”¢ÖĘŌģ³É±¾·Ö±šĪŖ![]() ĶņŌŖ”¢
ĶņŌŖ”¢![]() ĶņŌŖ£®
ĶņŌŖ£®
![]() Č·¶Ø
Č·¶Ø![]() µÄÖµ£¬²¢Ēó
µÄÖµ£¬²¢Ēó![]() Äź²śĘ·×ܳɱ¾ĪŖ¶ąÉŁĶņŌŖ£»
Äź²śĘ·×ܳɱ¾ĪŖ¶ąÉŁĶņŌŖ£»
![]() ĪŖ½µµĶ×ܳɱ¾£¬øĆ¹«Ė¾
ĪŖ½µµĶ×ܳɱ¾£¬øĆ¹«Ė¾![]() Äź¼°
Äź¼°![]() ÄźŌö¼ÓĮĖ¼¼Źõ³É±¾Ķ¶Čė£¬Č·±£ÕāĮ½Äź¼¼Źõ³É±¾¶¼±ČĒ°Ņ»ÄźŌö¼ÓŅ»øöĻąĶ¬µÄ°Ł·ÖŹż
ÄźŌö¼ÓĮĖ¼¼Źõ³É±¾Ķ¶Čė£¬Č·±£ÕāĮ½Äź¼¼Źõ³É±¾¶¼±ČĒ°Ņ»ÄźŌö¼ÓŅ»øöĻąĶ¬µÄ°Ł·ÖŹż![]() £¬ÖĘŌģ³É±¾ŌŚÕāĮ½ÄźĄļ¶¼±ČĒ°Ņ»Äź¼õÉŁŅ»øöĻąĶ¬µÄ°Ł·ÖŹż
£¬ÖĘŌģ³É±¾ŌŚÕāĮ½ÄźĄļ¶¼±ČĒ°Ņ»Äź¼õÉŁŅ»øöĻąĶ¬µÄ°Ł·ÖŹż![]() £»Ķ¬Ź±ĪŖĮĖĄ©“óĻśŹŪĮ棬
£»Ķ¬Ź±ĪŖĮĖĄ©“óĻśŹŪĮ棬![]() ÄźµÄĻśŹŪ³É±¾½«ŌŚ
ÄźµÄĻśŹŪ³É±¾½«ŌŚ![]() ÄźµÄ»ł“”ÉĻĢįøß
ÄźµÄ»ł“”ÉĻĢįøß![]() £¬¾¹żŅŌÉĻ±äøļ£¬Ō¤¼Ę
£¬¾¹żŅŌÉĻ±äøļ£¬Ō¤¼Ę![]() ÄźøĆ²śĘ·×ܳɱ¾“ļµ½
ÄźøĆ²śĘ·×ܳɱ¾“ļµ½![]() ÄźøĆ²śĘ·×ܳɱ¾µÄ
ÄźøĆ²śĘ·×ܳɱ¾µÄ![]() £¬Ēó
£¬Ēó![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABCDÖŠ£¬AEĘ½·Ö”ĻBAD£¬½»BCÓŚE£¬DE”ĶAE£¬ĻĀĮŠ½įĀŪ£ŗ£ŗ¢ŁDEĘ½·Ö”ĻADC£»¢ŚEŹĒBCµÄÖŠµć£»¢ŪAD=2CD£»¢ÜĢŻŠĪADCEµÄĆ껿Óė”÷ABEµÄĆ껿±ČŹĒ3£ŗ1£¬ĘäÖŠÕżČ·µÄ½įĀŪµÄøöŹżÓŠ£Ø £©

A. 4 B. 3 C. 2 D. 1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬AEĘ½·Ö”ĻBAD£¬½»BCÓŚE£¬¹żE×öEF”ĶADÓŚF£¬Į¬½ÓBF½»AEÓŚP£¬Į¬½ÓPD£®

£Ø1£©ĒóÖ¤£ŗĖıߊĪABEFŹĒÕż·½ŠĪ£»
£Ø2£©Čē¹ūAB=6£¬AD=8£¬Ēótan”ĻADPµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬µćCĪŖ”ŃOÉĻŅ»µć£¬AEŗĶ¹żµćCµÄĒŠĻß»„Ļą“¹Ö±£¬“¹×ćĪŖE£¬AE½»”ŃOÓŚµćD£¬Ö±ĻßEC½»ABµÄŃÓ³¤ĻßÓŚµćP£¬Į¬½ÓAC£¬BC£¬PB£ŗPC=1£ŗ2£®

£Ø1£©ĒóÖ¤£ŗACĘ½·Ö”ĻBAD£»
£Ø2£©Ģ½¾æĻ߶ĪPB£¬ABÖ®¼äµÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©ČōAD=3£¬Ēó”÷ABCµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
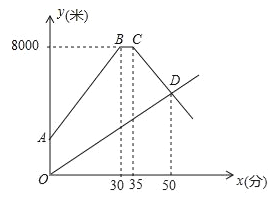
”¾ĢāÄæ”æ¼×ŅŅĮ½µŲĻą¾ą8000Ć×£®ÕÅĮĮĘļ×ŌŠŠ³µ“Ó¼×µŲ³ö·¢ŌČĖŁĒ°ĶłŅŅµŲ£¬³ö·¢10·ÖÖÓŗó£¬ĄīĪ°²½ŠŠ“Ó¼×µŲ³ö·¢Ķ¬Ā·ŌČĖŁĒ°ĶłŅŅµŲ£®ÕÅĮĮµ½“ļŅŅµŲŗóŠŻĻ¢Ę¬æĢ£¬ŅŌŌĄ“µÄĖŁ¶Č“ÓŌĀ··µ»Ų£®ČēĶ¼ĖłŹ¾ŹĒĮ½ČĖĄė¼×µŲµÄ¾ąĄėy£ØĆ×£©ÓėĄīĪ°²½ŠŠŹ±¼äx£Ø·Ö£©Ö®¼äµÄŗÆŹżĶ¼Ļó£®
£Ø1£©ĒóĮ½ČĖĻąÓöŹ±ĄīĪ°ĄėŅŅµŲµÄ¾ąĄė£»
£Ø2£©ĒėÄćÅŠ¶Ļ£ŗµ±ÕÅĮĮ·µ»Ųµ½¼×µŲŹ±£¬ĄīĪ°ŹĒ·ńµ½“ļŅŅµŲ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com