【答案】
分析:(1)当P在AB边上运动时(如图1),过B作BE垂直于AD,由梯形ABCD为等腰梯形,由下底与上底之差的一半求出AE,在直角三角形ABE中,得到AE等于AB的一半,而AQ等于AP的一半,且夹角为公共角得到三角形APQ与三角形ABE相似,进而确定出PQ垂直于AD,由AP与AQ,利用勾股定理表示出PQ,由AQ与PQ乘积的一半即可表示出S与t的函数关系式,再由AB的长,除以P运动的速度求出P到B的时间,即可确定出t的范围;
(2)当点P在线段BC上运动时(如图2),过P作PE⊥AD,由(1)得得到PE的长,三角形APQ以AQ为底,PE为高,利用三角形的面积公式表示出S与t的关系式即可,由AB+BC的长除以P运动的速度,求出时间t的值,即可确定出此时t的范围;
(3)当点P在线段CD上运动时(如图3),过P作PE垂直于AD,CF垂直于AD,可得出CF的长,由三角形PDE与三角形CDF相似,由相似得比例,将各自的值代入表示出PE,三角形APQ以AQ为底,PE为高,利用三角形的面积公式表示出此时S与t的关系式,并由AB+BC+CD的长除以P运动的速度,求出此时t的范围,分别求出三解析式中S的最大值,比较大小即可得到S的最大值.
解答:
解:(1)P在AB上运动时,过B作BE⊥AD,如图1所示,
∵AD=8cm,BC=2cm,AB=CD=6cm,
∴AE=

(AD-BC)=3cm,
在Rt△ABE中,AB=6cm,AE=3cm,即AB=2AE,
又∵AP=2tcm,AQ=tcm,即AP=2AQ,且∠A=∠A,
∴△APQ∽△ABE,
∴∠PQA=∠BEA=90°,
在Rt△APQ中,根据勾股定理得:PQ=
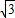
tcm,
则S=
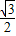
t
2,(0<t≤3);
故答案为:S=

t
2;0<t≤3;
(2)P在BC上运动时,过P作PE⊥AD,如图2所示,
由(1)得到PE=3

cm,又AQ=tcm,
则S=

AQ•PE=

t(3<t≤4);
(3)P在CD上运动时,过P作PE⊥AD,CF⊥AD,如图3所示,
可得△PDE∽△CDF,由(1)得到CF=3

,
则

=

,即
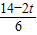
=
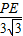
,
解得PE=(7-t)

cm,又AQ=tcm,
则S=

t(7-t)=-
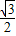
t
2+

t(4≤t<7),
综上,P在AB上运动时,当t=3时,S取最大值,S最大为


;
P在BC上运动时,当t=4时,S取最大值,S最大为6
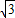
;
P在CD上运动时,当t=4时,S取最大值,S最大为6
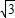
,
则点P在整个运动过程中,当t取4时,S的值最大,为6

.
点评:此题考查了相似型综合题,涉及的知识有:相似三角形的判定与性质,勾股定理,等腰梯形的性质,以及一次、二次函数的性质,灵活运用相似三角形的判定与性质是解本题的关键.


 (AD-BC)=3cm,
(AD-BC)=3cm,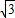 tcm,
tcm,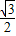 t2,(0<t≤3);
t2,(0<t≤3); t2;0<t≤3;
t2;0<t≤3; cm,又AQ=tcm,
cm,又AQ=tcm, AQ•PE=
AQ•PE= t(3<t≤4);
t(3<t≤4); ,
, =
= ,即
,即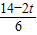 =
=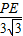 ,
, cm,又AQ=tcm,
cm,又AQ=tcm, t(7-t)=-
t(7-t)=-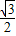 t2+
t2+ t(4≤t<7),
t(4≤t<7),
 ;
;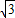 ;
;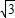 ,
, .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,在梯形ABCD中,AB∥CD,E是AB边上的点,给出下面三个论断:①AD=BC;②DE=CE;③AE=BE.请你以其中的两个论断为条件,填入“已知”栏中,以一个论断作为结论,填入“求证”栏中,使之成为一个正确的命题,并证明之.
如图,在梯形ABCD中,AB∥CD,E是AB边上的点,给出下面三个论断:①AD=BC;②DE=CE;③AE=BE.请你以其中的两个论断为条件,填入“已知”栏中,以一个论断作为结论,填入“求证”栏中,使之成为一个正确的命题,并证明之.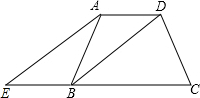 如图,在梯形ABCD中,AD∥BC,AD=AB,过点A作AE∥DB交CB的延长线于点E.
如图,在梯形ABCD中,AD∥BC,AD=AB,过点A作AE∥DB交CB的延长线于点E.