
 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的坐标为(45,8).
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的坐标为(45,8). 分析 以正方形最外边上的点为准考虑,点的总个数等于最右边上的横坐标的平方,且横坐标为奇数时最后一个点在x轴上,为偶数时,从x轴上的点开始排列,求出与2017最接近的平方数为2025,然后写出第2017个点的坐标即可.
解答 解:根据图形可知:以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,
如:右下角的点的横坐标为1,共有1个,即1=12,
右下角的点的横坐标为2时,共有4个,即4=22,
右下角的点的横坐标为3时,共有9个,即9=32,
…
右下角的点的横坐标为n时,共有n2个,
∵442=1936,452=2025,
根据规律可知:当n为奇数时,最后以点(n,0)结束;当n为偶数时,最后以点(1,n-1)结束;
∵n=45为奇数,
∴该正方形每一边上有45个点,且最后一个点的坐标为(45,0),是第2025个点,
∴第2017个点是从第2025个点向上数第8个点,
∴第2017个点的坐标为(45,8);
故答案为:(45,8).
点评 本题考查了点的坐标的规律变化,从正方形的观点考虑求解更简便,本题的突破口就是每一个正方形的最右边的点,要注意正方形的右边的点的横坐标是奇数还是偶数时,点的规律的不同.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:选择题
| A. | x1=-3 x2=-1 | B. | x1=1 x2=3 | C. | x1=-1 x2=3 | D. | x1=-3 x2=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
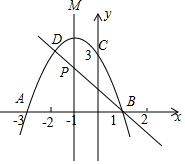 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
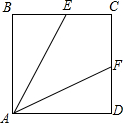 如图,点E、F位于正方形ABCD边BC、CD上.
如图,点E、F位于正方形ABCD边BC、CD上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,CE是∠DCB的平分线,交DA的延长线于点E,F是AD的中点,若AB=6,BC=4,则EF:FD等于( )
如图,在?ABCD中,CE是∠DCB的平分线,交DA的延长线于点E,F是AD的中点,若AB=6,BC=4,则EF:FD等于( )| A. | 2;1 | B. | 3:2 | C. | 4:3 | D. | 4:1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com