
【题目】在平面直角坐标系中,BC∥OA,BC=3,OA=6,AB=3![]()
(1)直接写出点B的坐标
(2)已知D.E分别为线段OC.OB上的点,OD=5,OE=2BE,直线DE交x轴于点F,求直线DE的解析式
(3)在(2)的条件下,点M是直线DE上的一点,在x轴上方是否存在另一个点N,使以O.D.M.N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由。

【答案】(1)B(3,6) (2) y=-![]() x+5 (3) 存在N1 (4,8) N2 (-5,2.5)N3(-2
x+5 (3) 存在N1 (4,8) N2 (-5,2.5)N3(-2![]() ,
,![]() )
)
【解析】分析:(1)作BH⊥x轴于点H,则四边形OHBC为矩形,则OH=CB=3,进而可求得AH的长,在Rt△ABH中,根据勾股定理即可求出BH的长,由此可得B点坐标;
(2)作EG⊥x轴于点G,则EG∥BH,易得![]() 根据相似三角形的对应边成比例可求出EG、OG的长,即可得到E点的坐标,进而可用待定系数法求出直线DE的解析式;
根据相似三角形的对应边成比例可求出EG、OG的长,即可得到E点的坐标,进而可用待定系数法求出直线DE的解析式;
(3)此题应分情况讨论:
①以OD、ON为边的菱形ODMN,根据直线DE的解析式可求出F点的坐标,即可得到OF的长;过M作![]() 轴于P,通过构建的相似三角形可求出M点的坐标,将M点向下平移OD个单位即可得到N点的坐标;
轴于P,通过构建的相似三角形可求出M点的坐标,将M点向下平移OD个单位即可得到N点的坐标;
②以OD、OM为边的菱形ODNM,此时MN∥y轴,延长NM交x轴于P,可根据直线DE的解析式用未知数设出M点的坐标,进而可在![]() 中,由勾股定理求出M点的坐标,将M点向上平移OD个单位即可得到N点的坐标;
中,由勾股定理求出M点的坐标,将M点向上平移OD个单位即可得到N点的坐标;
③以OD为对角线的菱形OMCN,根据菱形对角线互相垂直平分的性质即可求得M、N的纵坐标,将M点纵坐标代入直线DE的解析式中即可求出M点坐标,而M、N关于y轴对称,由此可得到N点的坐标.
详解:(1)作BH⊥x轴于点H,则四边形OHBC为矩形,
∴OH=CB=3,
∴AH=OAOH=63=3,
在Rt△ABH中,![]()
∴点B的坐标为(3,6);
(2)作EG⊥x轴于点G,则EG∥BH,
∴△OEG∽△OBH,
∴![]()
又∵OE=2EB,
∴![]() ∴
∴![]()
∴OG=2,EG=4,
∴点E的坐标为(2,4),
又∵点D的坐标为(0,5),
设直线DE的解析式为y=kx+b,
则![]()
解得![]()
∴直线DE的解析式为:![]()
(3)答:存在;
①如图1,当OD=DM=MN=NO=5时,四边形ODMN为菱形.作MP⊥y轴于点P,则MP∥x轴,
∴![]()
又∵当y=0时,![]()
解得x=10,
∴F点的坐标为(10,0),
∴OF=10,
在Rt△ODF中,![]()
∴![]()
∴![]()
∴点M的坐标为![]()
∴点N的坐标为![]()
②如图2,当OD=DN=NM=MO=5时,四边形ODNM为菱形,延长NM交x轴于点P,则MP⊥x轴.

∵点M在直线![]() 上,
上,
∴设M点坐标为![]()
在Rt△OPM中,![]()
∴![]()
解得:![]() (舍去),
(舍去),
∴点M的坐标为(4,3),
∴点N的坐标为(4,8);
③如图3,当OM=MD=DN=NO时,四边形OMDN为菱形,连接NM,交OD于点P,则NM与OD互相垂直平分,

∴![]()
∴![]()
∴![]()
∴![]()
∴点N的坐标为![]()
综上所述,x轴上方的点N有三个,分别为![]()


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形纸片ABCD中,AB=3,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则图中重叠部分的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
(1)求证:AB=AF;
(2)若BC=2AB,∠BCD=110°,求∠ABE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标为
的坐标为![]() .
.

①把![]() 向上平移5个单位后得到对应的
向上平移5个单位后得到对应的![]() ,画出
,画出![]() ,并写出
,并写出![]() 的坐标;
的坐标;
②以原点![]() 为对称中心,画出
为对称中心,画出![]() 与关于原点
与关于原点![]() 对称的
对称的![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
③以原点O为旋转中心,画出把![]() 顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
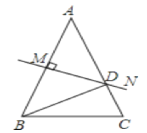
【题目】已知:如图,AB=AC,∠A=36°,AB的垂直平分线交AC于D,则下列结论:①∠C=72°;②BD是∠ABC的平分线;③△ABD是等腰三角形;④△BCD是等腰三角形,其中正确的有____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式A=x2+3xy+x﹣12,B=2x2﹣xy+4y﹣1
(1)当x=y=﹣2时,求2A﹣B的值;
(2)若2A﹣B的值与y的取值无关,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
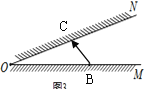
【题目】如图,已知∠O=30°,点B是OM边上的一个点光源,在边ON上放一平面镜.光线BC经
过平面镜反射后,反射光线与边OM的交点记为E,则△OCE是等腰三角形的个数有( )
A. 1个 B. 2个 C. 3个 D. 3个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解“停车难”问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图。按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入。(其中AB=9m,BC=0.5m)为标明限高,请你根据该图计算CE。(精确到0.1m)(参考数值![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
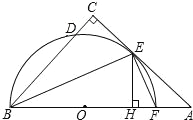
(1)求证:AC是⊙O的切线.
(2)过点E作EH⊥AB于点H,求证:CD=HF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com