练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知一个二次函数的图像经过点（4，1）和（，6）．
    （1）求这个二次函数的解析式；
    （2）求这个二次函数图像的顶点坐标和对称轴．

    (1);(2)顶点坐标是（2，-3）,对称轴是直线．

    解析试题分析：（1）利用待定系数法确定二次函数的解析式；
    （2）把（1）中得到的解析式配成顶点式，然后根据二次函数的性质确定顶点坐标和对称轴
    试题解析：
    （1）由题意，得
    解这个方程组，得
    ∴所求二次函数的解析式是．
    （2）顶点坐标是（2，-3）．
    对称轴是直线．
    考点：1.待定系数法求二次函数解析式；2.二次函数的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    如图，直线y＝x＋3与坐标轴分别交于A，B两点，抛物线y＝ax2＋bx－3a经过点A，B，顶点为C，连接CB并延长交x轴于点E，点D与点B关于抛物线的对称轴MN对称.

    （1）求抛物线的解析式及顶点C的坐标；
    （2）求证：四边形ABCD是直角梯形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知抛物线与x轴交于A（－1，0）、E（3，0）两点，与y轴交于点B（0，3）。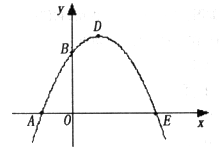

    （1）求抛物线的解析式；
    （2）设抛物线顶点为D，求四边形AEDB的面积；
    （3）△AOB与△DBE是否相似？如果相似，请给以证明；如果不相似，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    某农户生产经销一种农副产品，已知这种产品的成本价为20元/千克．市场调查发现，该产品每天的销售量w （千克）与销售价x （元/千克）有如下关系：w=﹣2x+80．设这种产品每天的销售利润为y （元）．
    （1）求y与x之间的函数关系式，自变量x的取值范围；
    （2）当销售价定为多少元时，每天的销售利润最大？最大利润是多少？
    （3）如果物价部门规定这种产品的销售价不得高于28元/千克，该农户想要每天获得150元的销售利润，销售价应定为多少元？（参考关系：销售额=售价×销量，利润=销售额﹣成本）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知抛物线经过点（3,0）,（－1,0）．
    （1）求抛物线的解析式;
    （2）求抛物线的顶点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，抛物线y=x2+mx+n交x轴于A、B两点，交y轴于点C，点P是它的顶点，点A的坐标是（1，0），点B的坐标是（﹣3，0）．

    （1）求m、n的值；
    （2）求直线PC的解析式．
    [温馨提示：抛物线y=ax2+bx+c（a≠0）的顶点坐标为（﹣，）]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    跳绳时,绳甩到最高处时的形状是抛物线．正在甩绳的甲．乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0．9米,身高为1．4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E．以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为y=ax2＋bx＋0．9．
    （1）求该抛物线的解析式 ．

    （2）如果小华站在OD之间,且离点O的距离为3米,当绳子甩到最高处时刚好通过他的头顶,小华的身高为               ;
    （3）如果身高为1．4米的小丽站在OD之间,且离点O的距离为t米, 绳子甩到最高处时超过她的头顶,请结合图像,写出t的取值范围                  ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知二次函数的图象经过点A（2，－3），B（－1，0）．
    （1）求二次函数的解析式；
    （2）观察函数图象，要使该二次函数的图象与轴只有一个交点，应把图象沿轴向上平移几个单位？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    在某市开展的环境创优活动中，某居民小区要在一块靠墙（墙长15米）的空地上修建一个矩形花园ABCD，花园的一边靠墙，另三边用总长为40m的栅栏围成，若设花园与墙平行的一边长为x(m)，花园的面积为y(m2)。
    （1）求y与x之间的函数关系式，并写出自变量x的取值范围；
    （2）满足条件的花园面积能达到200m2吗？若能，求出此时x的值，若不能，说明理由：
    （3）根据(1)中求得的函数关系式，判断当x取何值时，花园的面积最大？最大面积是多少？

    查看答案和解析>>

    同步练习册答案