
 MN-ND
MN-ND NC
NC 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 5 |
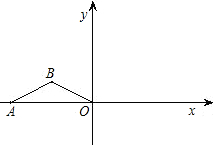 转90°,得到△A1B1O,再继续旋转90°,得到△A2B2O.抛物线y=ax2+bx+3经过B、B1两点.
转90°,得到△A1B1O,再继续旋转90°,得到△A2B2O.抛物线y=ax2+bx+3经过B、B1两点.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
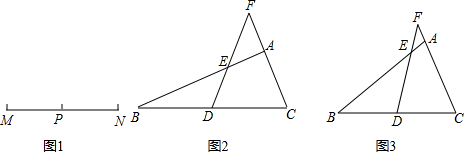 变,若BE=CF的结论仍然成立,请写出△AEF必须满足的条件,并加以证明.
变,若BE=CF的结论仍然成立,请写出△AEF必须满足的条件,并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:
 四跳落点于P4,P4与P3关于竹竿l成轴对称;以此跃下去,若每25跳可以休息一次.
四跳落点于P4,P4与P3关于竹竿l成轴对称;以此跃下去,若每25跳可以休息一次.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com