
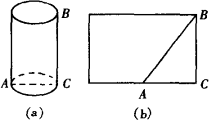
如图(a)所示的几何体是一个圆柱体,它的高为20,底面半径为6.7.如果一只蚂蚁要自圆柱体下底面的A点,沿圆柱形曲面爬到与A相对的上底面B点.求爬行的最短路线的长度.
科目:初中数学 来源: 题型:
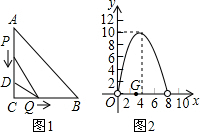 Q的最大面积;若不存在,请说明理由.
Q的最大面积;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
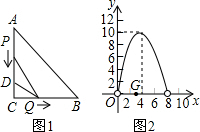 Q的最大面积;若不存在,请说明理由.
Q的最大面积;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2009年重庆市中考数学权威预测试卷(三)(解析版) 题型:解答题
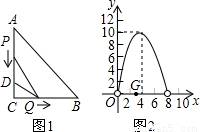
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com