
【题目】某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
类型 价格 | 进价(元/盏) | 售价(元/盏) |
A型 | 25 | 45 |
B型 | 40 | 70 |
(1)若商场进货款为3100元,则这两种台灯各购进多少盏?
(2)若商场在3200元的限额内购进这两种台灯,且A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
【答案】(1)应购进A型台灯60盏,B型台灯40盏;(2)商场购进A型台灯54盏,B型台灯46盏,销售完这批台灯时获利最多,此时利润为2460元.
【解析】
(1)设商场应购进A型台灯x盏,则B型台灯为(100x)盏,根据“商场进货款为3100元”列出关于x的一元一次方程,即可求解;
(2)设商场销售完这批台灯可获利y元,列出y关于x的一次函数解析式,根据“商场在3200元的限额内购进这两种台灯,且A型台灯的进货数量不超过B型台灯数量的3倍”列出关于x的不等式,求出x的范围,进而根据一次函数的性质,即可求解.
(1)设商场应购进A型台灯x盏,则B型台灯为(100x)盏,
根据题意得:25x+40(100x)=3100,
解得:x=60,
∴10060=40(盏),
答:应购进A型台灯60盏,B型台灯40盏;
(2)设商场销售完这批台灯可获利y元,
根据题意得:y=(4525)x+(7040)(100x)=20x+300030x=10x+3000,
即:y=10x+3000,
∵商场在3200元的限额内购进这两种台灯,且A型台灯的进货数量不超过B型台灯数量的3倍,
∴25x+40(100x)≤3200且x≤3(100x),
∴![]() ≤x≤75,
≤x≤75,
∵k=10<0,y随x的增大而减小,
∴当x=54时,y最大值=10×54+3000=2460(元),
答:商场购进A型台灯54盏,B型台灯46盏,销售完这批台灯时获利最多,此时利润为2460元.


科目:初中数学 来源: 题型:
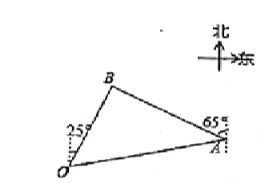
【题目】中国海军亚丁湾护航十年,中国海军被亚丁湾上来往的各国商船誉为“值得信赖的保护伞”.如图,在一次护航行动中,我国海军监测到一批可疑快艇正快速向护航的船队靠近,为保证船队安全,我国海军迅速派出甲、乙两架直升机分别从相距40海里的船队首(![]() 点)尾(
点)尾(![]() 点)前去拦截,8分钟后同时到达
点)前去拦截,8分钟后同时到达![]() 点将可疑快艇驱离.己知甲直升机每小时飞行180海里,航向为北偏东
点将可疑快艇驱离.己知甲直升机每小时飞行180海里,航向为北偏东![]() ,乙直升机的航向为北偏西
,乙直升机的航向为北偏西![]() ,求乙直升机的飞行速度(单位:海里/小时).
,求乙直升机的飞行速度(单位:海里/小时).
查看答案和解析>>
科目:初中数学 来源: 题型:
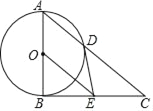
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D,过圆心O作OE∥AC,交BC于点E,连接DE.
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:2DE2=CDOE;
(3)若tanC=![]() ,DE=
,DE=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数y=x+b与反比例函数y=![]() 图象,在第二象限内有两个交点,则k______0,b_______0,(用“>”、“<”、“=”填空)
图象,在第二象限内有两个交点,则k______0,b_______0,(用“>”、“<”、“=”填空)
查看答案和解析>>
科目:初中数学 来源: 题型:
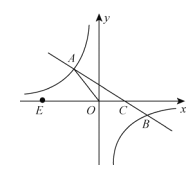
【题目】如图,在平面直角坐标系xoy中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出一次函数值大于反比例函数自变量x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,D为BC上一点,且DE⊥AB于E,若DE=CD,AB=8cm,则△DEB的周长为( )
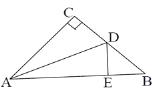
A.4cmB.8cmC.10cmD.14cm
查看答案和解析>>
科目:初中数学 来源: 题型:
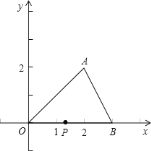
【题目】如图,已知![]() ,
,![]() .动点
.动点![]() 在线段
在线段![]() 上移动,过点
上移动,过点![]() 作直线
作直线![]() 与
与![]() 轴垂直.
轴垂直.
![]() 设
设![]() 中位于直线
中位于直线![]() 左侧部分的面积为
左侧部分的面积为![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 试问是否存在点
试问是否存在点![]() ,使直线
,使直线![]() 平分
平分![]() 的面积?若有,求出点
的面积?若有,求出点![]() 的坐标;若无,请说明理由.
的坐标;若无,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
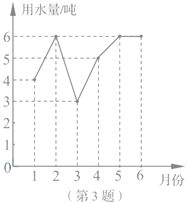
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com