
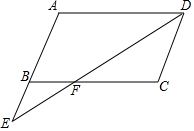
 如图,在?ABCD中,点E是AB延长线上一点,连结DE与BC相交于点F,且$\frac{BF}{FC}$=$\frac{1}{2}$.
如图,在?ABCD中,点E是AB延长线上一点,连结DE与BC相交于点F,且$\frac{BF}{FC}$=$\frac{1}{2}$.分析 (1)根据三角形相似和平行四边形的性质可以得到$\frac{BE}{AE}$的值;
(2)要求?ABCD的面积,只要求出CF与BC的比值即可,然后根据三角形相似和平行四边形的性质可以得到?ABCD的面积.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴△BFE∽△CFD,
∴$\frac{BE}{CD}=\frac{BF}{FC}$,
∵$\frac{BF}{FC}$=$\frac{1}{2}$,
∴$\frac{BE}{CD}=\frac{1}{2}$,
∴$\frac{BE}{AE}=\frac{1}{3}$;
(2))∵四边形ABCD是平行四边形,$\frac{BF}{FC}$=$\frac{1}{2}$,
∴AB∥CD,AB=CD,
∴△BFE∽△CFD,
∴$\frac{{S}_{△BFE}}{{S}_{△CFD}}=(\frac{1}{2})^{2}=\frac{1}{4}$,
∵△BEF的面积是1,
∴△CDF的面积是4,
∵$\frac{CF}{CB}=\frac{2}{3}$,
∴$\frac{{S}_{△CFD}}{{S}_{平行四边形ABCD}}=\frac{CF}{BC}$=$\frac{2}{3}$,
∴?ABCD的面积是6.
点评 本题考查平行四边形的性质和相似三角形的性质和判定,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:选择题
| A. | 20 | B. | 119 | C. | 120 | D. | 319 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8,.过点B作⊙O的切线BD,过点A作AD⊥BD,垂足为D.
如图,已知⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8,.过点B作⊙O的切线BD,过点A作AD⊥BD,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B,连结BC.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B,连结BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com