
ij��˾��2009�꿪ʼͶ�뼼�������ʽ𣬾������Ľ������Ʒ�������ɱ����Ͻ��ͣ��������������
| ��� | 2009 | 2010 | 2011 | 2012 |
| Ͷ�뼼���ʽ�x����Ԫ�� | 2.5 | 3 | 4 | 4.5 |
| ��Ʒ�ɱ�y����Ԫ/���� | 7.2 | 6 | 4.5 | 4 |
��1��������������ϵy=
��2���ٽ���0.4��Ԫ ��0.63��Ԫ
���������������1������ʵ������������ص�������⣬�����ų�����֪��Ϊ���������������ô���ϵ������⼴�ɣ�
��2��ֱ�Ӱ�x=5��Ԫ��y=3.2�ֱ���뺯������ʽ������⣮
�⣺��1���ɱ�������֪��x��y��ϵ��
xy=2.5��7.5=3��6=4��4.5=4.5��4=18
��xy=18
��x��y����һ�κ�����ϵ
����������Ƿ�����������ϵy= ��
��
��2���ٵ�x=5��Ԫʱ��y=3.6��
4��3.6=0.4����Ԫ����
�������ɱ�ÿ����2009�꽵��0.4��Ԫ��
�ڵ�y=3.2��Ԫʱ��3.2= ��
��
��x=5.625��1�֣�
��5.625��5=0.625��0.63����Ԫ��
�Լ��Ͷ��0.63��Ԫ��
��������Ҫ�����˺�����ʵ��Ӧ�ã�����Ĺؼ��Ǹ���ʵ�������г�������ϵʽ����ʵ���������ҵ���Ӧ�ı�����ֵ�����ô���ϵ���������������ʽ���ٸ����Ա�����ֵ�����Ӧ�ĺ���ֵ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
һ�κ��� ��ͼ���뷴��������
��ͼ���뷴�������� ��ͼ����A��-2��1����B��1��n�����㣮
��ͼ����A��-2��1����B��1��n�����㣮
��1����ȷ������������������һ�κ����ı���ʽ��
��2�����OAB�������
��3��д������������ֵ����һ�κ���ֵ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У�һ�κ��� ��k��0����ͼ���뷴��������
��k��0����ͼ���뷴�������� ��m��0����ͼ����A��B���㣬��x�ύ��C�㣬��A������Ϊ��n��6������C������Ϊ����2��0������
��m��0����ͼ����A��B���㣬��x�ύ��C�㣬��A������Ϊ��n��6������C������Ϊ����2��0������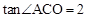 ��
��
��1����÷�����������һ�κ����Ľ���ʽ��
��2�����B�����ꣻ
��3����x�������E��ʹ��ACEΪֱ�������Σ���ֱ��д����E�����꣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��һ�κ���y=ax+b��ͼ���뷴�������� ��ͼ����A����2��m����B
��ͼ����A����2��m����B
��4����2�����㣬��x�ύ��C�㣬��A��AD��x����D��
��1���������������Ľ���ʽ��
��2�����ADC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��2013���Ĵ�����8�֣���ͼ����֪���� �뷴��������
�뷴�������� ��x��0����ͼ���ڵ�A����
��x��0����ͼ���ڵ�A���� ��ͼ������ƽ��6����λ����˫����
��ͼ������ƽ��6����λ����˫���� ���ڵ�B����x�ύ�ڵ�C��
���ڵ�B����x�ύ�ڵ�C��
��1�����C�����ꣻ
��2���� �����������Ľ���ʽ��
�����������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪��O��ƽ��ֱ������ϵ��ԭ�㣬ֱ��y=��x+m+n��˫����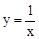 ����������ͬ�ĵ�A��m��n����m��2����B��p��q����ֱ��y=��x+m+n��y�ύ�ڵ�C�����OBC�����S��ȡֵ��Χ��
����������ͬ�ĵ�A��m��n����m��2����B��p��q����ֱ��y=��x+m+n��y�ύ�ڵ�C�����OBC�����S��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ������������ ��ͼ����һ�κ���y=mx+b��ͼ����A��1��3����B��n����1�����㣮
��ͼ����һ�κ���y=mx+b��ͼ����A��1��3����B��n����1�����㣮
��1������������һ�κ����Ľ���ʽ��
��2������ͼ��ش𣺵�xȡ��ֵʱ��������������ֵ����һ�κ�����ֵ��
��3�����AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ���ѡ��
��ͼ��ʾ����1+��2=180�㣬��3=100�㣬���4���ڣ�������
| A��100�� | B��90�� | C��80�� | D��70�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com