
【题目】如图,已知AB∥CD,若按图中规律继续下去,则∠1+∠2+…+∠n等于( )


A. n·180° B. 2n·180° C. (n-1)·180° D. (n-1)2·180°
【答案】C
【解析】
根据第1个图形∠1+∠2=180°,第2个图形∠1+∠2+∠3=2×180°,第,3个图形∠1+∠2+∠3+∠4=3×180°…,进而得出答案.
(1)∵AB∥CD,
∴∠1+∠2=180°(两直线平行,同旁内角互补);
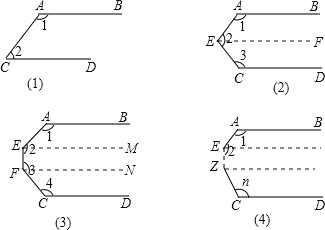
(2)过点E作一条直线EF平行于AB,
∵AB∥CD,
∴AB∥EF,CD∥EF,
∴∠1+∠AEF=180°,∠FEC+∠3=180°,
∴∠1+∠2+∠3=360°;
(3)过点E、F作EM、FN平行于AB,
∵AB∥CD,
∴AB∥EM∥FN∥CD,
∴∠1+∠AEM=180°,∠MEF+∠EFN=180°,∠NFC+∠4=180°;
∴∠1+∠2+3+∠4=540°;
(4)中,根据上述规律,显然作(n-1)条辅助线,运用(n-1)次两条直线平行,同旁内角互补.即可得到n个角的和是180°(n-1).
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为( )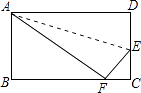
A.12
B.16
C.18
D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们在学习二次根式时,式子![]() 有意义,则x≥0;式子
有意义,则x≥0;式子![]() 有意义,则x≤0;若式子
有意义,则x≤0;若式子![]() +
+![]() 有意义,求x的取值范围. 这个问题可以转化为不等式组来解决,即求关于x的不等式组x≥0,x≤0的解集,解这个不等式组,得x=0. 请你运用上述的数学方法解决下列问题:
有意义,求x的取值范围. 这个问题可以转化为不等式组来解决,即求关于x的不等式组x≥0,x≤0的解集,解这个不等式组,得x=0. 请你运用上述的数学方法解决下列问题:
(1)式子![]() +
+![]() 有意义,求x的取值范围;
有意义,求x的取值范围;
(2)已知y=![]() +
+![]() -3,求
-3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市少年宫准备组织市区部分学校的中小学生到本市A,B,C,D,E五个旅游景区“一日游”,每名学生只能在五个景区中任选一个,为估算到各景区“一日游”的学生人数,少年宫随机抽取这些学校的部分学生,进行了“五个景区你最想去那里”的问卷调查,并把统计结果绘制成如图所示的统计图.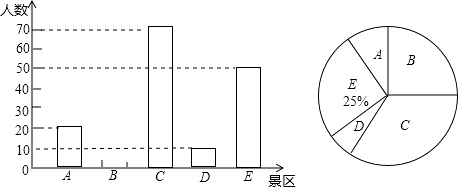
(1)求参加问卷调查的学生数,并将条形统计图补充完整;
(2)若参加“一日游”的学生为1000人,请估计到C景区“一日游”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
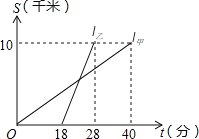
【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:
①乙比甲提前12分钟到达; ②甲的平均速度为15千米/小时;
③乙走了8km后遇到甲; ④乙出发6分钟后追上甲.
其中正确的有_____________(填所有正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)扇形统计图中![]() = , 分别计算三人民主评议的得分;
= , 分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,得分最高者将被选中,通过计算说明三人中谁被选中?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,教师出示某区篮球赛积分表如下:

(1)从表中可以看出,负一场积多少分,胜一场积多少分;
(2)请你帮忙算出二队胜了多少场?
(3)在这次比赛中,一个队胜场总积分能不能等于它的负场总积分?
(4)在计算五队、六队胜出场次的时候,老师还没等同学们计算出来就立刻说出了答案,老师解释说:“我是通过找到积分与胜场之间的数量关系求出来的”,请你说出其中的奥秘.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一条对角线平分一组对角的四边形叫做筝形.
探究:(1)如图1,四边形ABCD中,AB=BC,AD=DC,求证:四边形ABCD是筝形;
(2)下列关于筝形的性质表述正确的是 ;(把你认为正确的序号填在横线上)
①筝形的对角线互相垂直平分; ②筝形中至少有一对对角相等;
③筝形是轴对称图形; ④筝形的面积等于两条对角线长的积的一半.
应用:
(3)如图2,在筝形ABCD中,AB≠AD,若∠ABC=60°,∠ADC=30°,AD=4,请求出对角线BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com