
【题目】如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线![]() 经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4,则等边△AEF的边长为______.
经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4,则等边△AEF的边长为______.
 .
.
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:![]()
(2)如图,在矩形 ABCD 中,AE 平分∠BAD,交 BC 于点 E,过点 E 作 EF⊥AD 于点 F,求证:四边形ABEF 是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
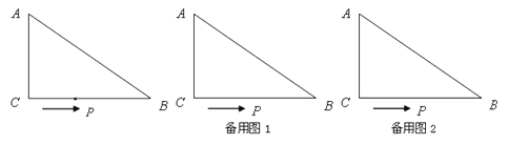
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.
(1)当t=1时,求△ACP的面积.
(2)t为何值时,线段AP是∠CAB的平分线?
(3)请利用备用图2继续探索:当t为何值时,△ACP是以AC为腰的等腰三角形?(直接写出结论)
(4)当p点在AB上运动时,线段CP值为整数的点有_______________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°.
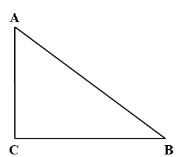
(1)作∠BAC的平分线,交BC于点D;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若BD=5,CD=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
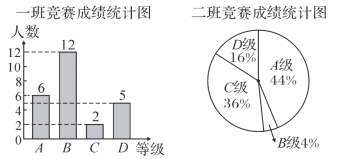
请你根据以上提供的信息解答下列问题
(1)此次竞赛中二班成绩在70分以上(包括70分)的人数为___;
(2)请你将表格补充完整:
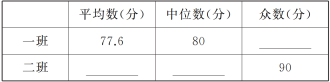
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
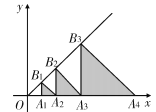
【题目】如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线y=x上,OA1=1,且△B1A1A2,△B2A2A3,△B3A3A4,…△Bn A n A n+1…分别是以A1,A2,A3,…An…为直角顶点的等腰直角三角形,则△B10A10A11的面积是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com