
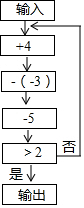
 ��ͼ��һ����ֵת������������ֵ�����������еij������㣬����һ������������2����������������Ƹ���ֻҪ����һ�顱������һ�����������������ҵڶ�������������2����������������Ƹ�����Ҫ�������顱���Դ����ƣ�
��ͼ��һ����ֵת������������ֵ�����������еij������㣬����һ������������2����������������Ƹ���ֻҪ����һ�顱������һ�����������������ҵڶ�������������2����������������Ƹ�����Ҫ�������顱���Դ����ƣ����� ��1�����ݳ�������õ���ʽ2+4-��-3��-5���㼴�ɣ�
��2�����ݳ�������õ���ʽ-1+4-��-3��-5=1���ٸ��ݳ�������õ���ʽ1+4-��-3��-5���㼴�ɣ�
��3�����ݳ�������õ���ʽx+4-��-3��-5=x+2��2���ٸ��ݳ�������õ���ʽx+2+4-��-3��-5=x+4��2���ⲻ��ʽ���ɵõ�x��ȡֵ��Χ���ɴ˼��ɽ�����⣮
��� �⣺��1��2+4-��-3��-5��=4��
��2��-1+4-��-3��-5=1��1+4-��-3��-5=3��
��3����������Ϊ-$\sqrt{2}$ʱ���𰸲�Ψһ������-2С��0�����������ɣ�
���� ���⿼�����������Ļ�����㣬����ؼ���Ū�����⣬������������������룬������һ��һ�����㣬�����ͻ�Ƶ㣬ȷ��һ����Ҫ�������顱�ſ�������������������ȡֵ��Χ��


 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�콭��ʡ�����о��꼶3���¿���ѧ�Ծ��������棩 ���ͣ���ѡ��
���к�����ͼ����ÿһ�������ڣ� 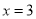 ֵ��
ֵ��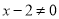 ֵ�������������ǣ� ��
ֵ�������������ǣ� ��
A. 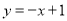 B.
B. 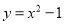 C.
C. 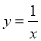 D.
D. 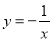
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | A��C | B�� | B��C | C�� | A+B=2C | D�� | A2+B2=C2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
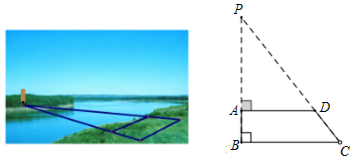
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
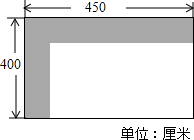 С������Ҫ���Լ��ҵ���̨���̵�ש�����������������ͼ��ͼֽ����ɫ����Ϊ������ȵ�һ����7���εĽ����ö���ʯС·���հײ���Ϊ��ש��������Ҫʹ�̵�ש�����Ϊ14ƽ���ף���ôС·�Ŀ���ӦΪ0.5�ף�
С������Ҫ���Լ��ҵ���̨���̵�ש�����������������ͼ��ͼֽ����ɫ����Ϊ������ȵ�һ����7���εĽ����ö���ʯС·���հײ���Ϊ��ש��������Ҫʹ�̵�ש�����Ϊ14ƽ���ף���ôС·�Ŀ���ӦΪ0.5�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��һ�������ֱ�����dzߣ��ֱ�30���45��ǣ�����ͼ��ʽ���ã���ͼ�С�AOB�Ķ���Ϊ��������
��һ�������ֱ�����dzߣ��ֱ�30���45��ǣ�����ͼ��ʽ���ã���ͼ�С�AOB�Ķ���Ϊ��������| A�� | 75�� | B�� | 95�� | C�� | 105�� | D�� | 120�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=-1 | B�� | x=0 | C�� | x=-$\sqrt{2}$ | D�� | x=2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com