
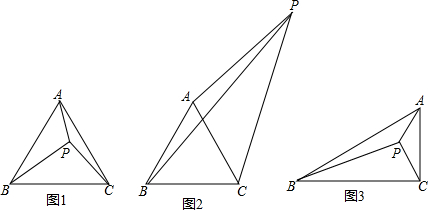
分析 (1)由旋转的性质得到△ADP为等边三角形,从而判断出△BPD为直角三角形,根据勾股定理计算即可;
(2)由旋转的性质得到△DAP是等边三角形,根据勾股定理得逆定理判断出△BPD为直角三角形,即可;
(3)作出△ABQ∽△ACP,判断出△APQ为直角三角形,从而得到△BPQ为直角三角形,根据勾股定理计算即可.
解答 解:(1)①依题意补全图形,如图1所示,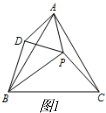
②由旋转有,AD=AP,BD=PC,∠DAB=∠PAC,
∴∠DAP=∠BAC=60°,
∴△ADP为等边三角形,
∴DP=PA=3,∠ADP=60°,
∵∠ADB=∠APC=150°,
∴∠BDP=90°,在Rt△BDP中,BD=4,DP=3,
根据勾股定理得,PB=5;
(2)如图2,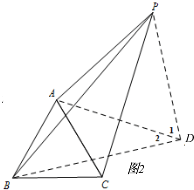
把△APC绕点A顺时针旋转,使点C与点B重合,得到△ADB,连接PD,
∴△APC≌△ADB,
∴AD=AP=3,DB=PC=4,∠PAC=∠DAB,∠APC=∠2,
∴∠DAP=∠BAC,
∵∠BAC=60°,
∴∠DAP=60°,
∴△DAP是等边三角形,
∴PD=3,∠1=60°,
∴PD2+DB2=32+42=52=PB2,
∴∠PDB=90°,
∴∠2=30°,
∴∠APC=30°;
(3)如图3
作△ABQ,使得:∠QAB=∠PAC,∠ABQ=∠ACP,则△ABQ∽△ACP,
∴∠AQB=∠APC=120°,
∵AB=2AC,
∴△ABQ与△ACP相似比为2,
∴AQ=2AP=2$\sqrt{3}$,BQ=2CP,∠QAP=∠QAB+∠BAP=∠PAC+∠BAP=∠BAC=60°,
∵$\frac{AQ}{AP}$=2,
∴∠APQ=90°,PQ=3,
∴∠AQP=30°
∴∠BQP=∠AQB-∠AQP=120°-30°=90°,
根据勾股定理得,BQ=$\sqrt{P{B}^{2}-P{Q}^{2}}$=4,
∴PC=$\frac{1}{2}$BQ=2.
点评 此题是几何变换综合题,主要考查了旋转的性质,直角三角形的性质和判断方法,勾股定理,直角三角形的判定是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 图象过点(3,2) | B. | 图象在第一、三象限 | ||
| C. | 当x>0时,y随x的增大而减少 | D. | 当x<0时,y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}×\sqrt{5}=\sqrt{10}$ | B. | $\sqrt{2}+\sqrt{5}=\sqrt{7}$ | C. | $\sqrt{18}÷\sqrt{2}=3$ | D. | $\sqrt{12}=2\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x3•x3=2x3 | B. | 4${\;}^{-2}=\frac{1}{16}$ | C. | $\sqrt{9}=±3$ | D. | (x3)2=x5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
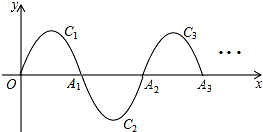 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,…如此进行下去,得到一条“波浪线”.若点P(41,m)在此“波浪线”上,则m的值为( )
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,…如此进行下去,得到一条“波浪线”.若点P(41,m)在此“波浪线”上,则m的值为( )| A. | 2 | B. | -2 | C. | 0 | D. | $\frac{9}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com