
【题目】已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D. 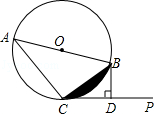
(1)求证:CB2=ABDB;
(2)若⊙O的半径为2,∠BCP=30°,求图中阴影部分的面积.
【答案】
(1)证明:如图,连接OC,
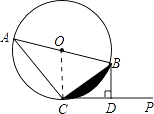
∵直线CP是⊙O的切线,
∴∠BCD+∠OCB=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠ACO+∠OCB=90°
∴∠BCD=∠ACO,
又∵∠BAC=∠ACO,
∴∠BCD=∠BAC,
又∵BD⊥CP
∴∠CDB=90°,
∴∠ACB=∠CDB=90°
∴△ACB∽△CDB,
∴ ![]() =ABDB
=ABDB
(2)解:∵直线CP是⊙O的切线,∠BCP=30°,
∴∠COB=2∠BCP=60°,
∴△OCB是正三角形,
∵⊙O的半径为2,
∴S△OCB= ![]() ,S扇形OCB=
,S扇形OCB= ![]() π,
π,
∴阴影部分的面积=S扇形OCB﹣S△OCB= ![]()
【解析】(1)由CP是⊙O的切线,得出∠BCD=∠BAC,AB是直径,得出∠ACB=90°,所以∠ACB=∠CDB=90°,得出结论△ACB∽△CDB;(2)求出△OCB是正三角形,阴影部分的面积=S扇形OCB﹣S△OCB , 即可得出答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O直径,半径OC⊥AB,连接AC,∠CAB的平分线AD分别交OC于点E,交 ![]() 于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( )
于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( ) 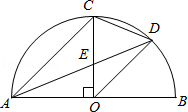
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点 ![]() 的坐标为
的坐标为![]() ,以 A 为顶点的
,以 A 为顶点的![]() 的两边始终与
的两边始终与 ![]() 轴交于
轴交于 ![]() 、
、![]() 两点(
两点(![]() 在
在 ![]() 左面),且
左面),且![]() .
.
(1)如图,连接![]() ,当
,当 ![]() 时,试说明:
时,试说明:![]() .
.

(2)过点 ![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,当
,当![]() 时,将
时,将![]() 沿
沿![]() 所在直线翻折,翻折后边
所在直线翻折,翻折后边![]() 交
交 ![]() 轴于点
轴于点 ![]() ,求点
,求点 ![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
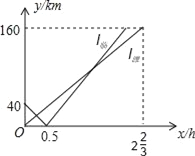
【题目】2015年5月中旬,中国和俄罗斯海军在地中海海域举行了代号为“海上联合﹣2015(1)”的联合军事演习,这是中国第一次地中海举行军事演习,也是这个海军距本土最远的一次军演,某天,“临沂舰”、“潍坊舰”两舰同时从A、B两个港口出发,均沿直线匀速驶向演习目标地海岛C,两舰艇都到达C岛后演习第一阶段结束,已知B刚位于A港、C港之间,且A、B、C在一条直线上,如图所示,l临、l潍分别表示“临沂舰”、“潍坊舰”离B港的距离行驶时间x(h)变化的图象.
(1)A港与C岛之间的距离为_____;
(2)分别求出“临沂舰”、“潍坊舰”的航速即相遇时行驶的时间;
(3)若“临沂舰”、“潍坊舰”之间的距离不超过2km时就属于最佳通讯距离,求出两舰艇在演习第一阶段处于最佳通讯距离时的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把下列各数填入相应的集合中.
2,0,2π,![]() ,2018,﹣0.030030003…
,2018,﹣0.030030003…
有理数集合:{___________________________________________…};
无理数集合:{___________________________________________…};
非负整数集合:{_________________________________________…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某服装专卖店去做社会调查,了解到该专卖店为了微励营业员的工作积极性,实行“月总收入=基本工资(固定)+计付奖金”的方法计算薪资,并获得如下信息;
营业员 | 小张 | 小王 |
月销售件数 | 200 | 150 |
月总收入/元 | 1400 | 1250 |
销售每件奖励a元,晋业员月基本工资为b元.
(1)列方程组求a,b的值.
(2)假设月销售件数为x,月总收入为y元,请写出y与x的函数关系式,并求出营业员小张上个月总收入是1700元时,小张上个月卖了多少件服装?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y与x﹣1成正比例,且当x=3时,y=4.
(1)求y与x之间的函数表达式;
(2)当x=﹣1时,求y的值;
(3)当﹣3<y<5时,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,
b满足 |a+2|+![]() =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3).
(1)求a,b的值及S三角形ABC;
(2)若点M在x轴上,且S三角形ACM=![]() S三角形ABC,试求点M的坐标.
S三角形ABC,试求点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com