
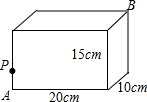
 如图,长方体的长为20cm,宽为10cm,高为15cm,棱上点P与顶点A相距5cm,一只蚂蚁如果要沿着长方体表面从点P爬到点B处,需要爬行的最短距离是多少?
如图,长方体的长为20cm,宽为10cm,高为15cm,棱上点P与顶点A相距5cm,一只蚂蚁如果要沿着长方体表面从点P爬到点B处,需要爬行的最短距离是多少? 分析 此题分两种情况比较最短距离:第一种是,先爬到棱的中点,再到B,此时转换到一个平面内,所走的路程是直角边为20cm、20cm的直角三角形的斜边的长;第二种是,此时转换到一个平面内,所走的路程是直角边为15cm,30cm的直角三角形的斜边的长;再根据勾股定理求出BP的长,比较出其大小即可.
解答 解:分两种情况比较最短距离:
如图1所示,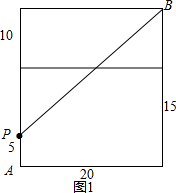
PB=$\sqrt{2{0}^{2}+2{0}^{2}}$=20$\sqrt{2}$,
如图2所示,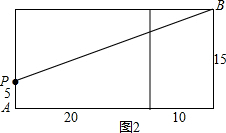
PB=$\sqrt{3{0}^{2}+1{0}^{2}}$=10$\sqrt{10}$,
∵10$\sqrt{10}$>20$\sqrt{2}$,
∴第一种情况短些,此时最短距离为22$\sqrt{2}$cm.
答:需要爬行的最短距离是20$\sqrt{2}$cm.
点评 本题考查的是平面展开-最短路径问题,根据题意画出图形,再根据勾股定理求解是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
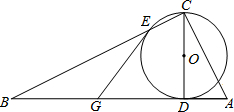 已知CD为Rt△ABC斜边AB上的高,以CD为直径的圆交BC于E点,交AC于F点,G为BD的中点.
已知CD为Rt△ABC斜边AB上的高,以CD为直径的圆交BC于E点,交AC于F点,G为BD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校中考模拟试题中有这样一道试题:
某校中考模拟试题中有这样一道试题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
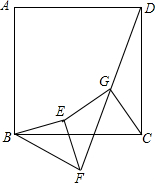 已知正方形ABCD,△BEF是等腰直角三角形(BE=EF),联结FD,在FD上取中点G,联结EC和CG,求证:
已知正方形ABCD,△BEF是等腰直角三角形(BE=EF),联结FD,在FD上取中点G,联结EC和CG,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com