
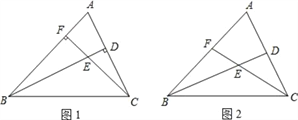
【题目】已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
(1)若BD⊥AC,CF⊥AB,如图1所示,试说明∠BAC+∠BEC=180°;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,试说明此时∠BAC与∠BEC的数量关系;
(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】分析:(1)根据余角的性质得到∠DEC=∠BAC,由于∠DEC+∠BEC=180°,即可得到结论;(2)根据角平分线的性质得到∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,于是得到结论;(3)作∠BEC的平分线EM交BC于M,由∠BAC=60°,得到∠BEC=90°+
∠ACB,于是得到结论;(3)作∠BEC的平分线EM交BC于M,由∠BAC=60°,得到∠BEC=90°+![]() ∠BAC=120°,求得∠FEB=∠DEC=60°,根据角平分线的性质得到∠BEM=60°,推出△FBE≌△EBM,根据全等三角形的性质得到EF=EM,同理DE=EM,即可得到结论.
∠BAC=120°,求得∠FEB=∠DEC=60°,根据角平分线的性质得到∠BEM=60°,推出△FBE≌△EBM,根据全等三角形的性质得到EF=EM,同理DE=EM,即可得到结论.
本题解析:

(1)∵BD⊥AC,CF⊥AB,
∴∠DCE+∠DEC=∠DCE+∠FAC=90°,
∴∠DEC=∠BAC,∠DEC+∠BEC=180°,
∴∠BAC+∠BEC=180°;
(2)∵BD平分∠ABC,CF平分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,∠BEC=180°(∠EBC+∠ECB)=180°
∠ACB,∠BEC=180°(∠EBC+∠ECB)=180°![]() (∠ABC+∠ACB)=180
(∠ABC+∠ACB)=180![]() (180°∠BAC)=90°+
(180°∠BAC)=90°+![]() ∠BAC,
∠BAC,
(3)作∠BEC的平分线EM交BC于M,
∵∠BAC=60°,
∴∠BEC=90°+![]() ∠BAC=120°,
∠BAC=120°,
∴∠FEB=∠DEC=60°,
∵EM平分∠BEC,
∴∠BEM=60°,
在△FBE与△EBM中,
∠FBE=∠EBMBE=BE∠FEB=∠MEB,
∴△FBE≌△EBM,
∴EF=EM,同理DE=EM,
∴EF=DE.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】平行四边形![]() 中,对角线
中,对角线![]() ,
, ![]() 相交于点
相交于点![]() ,若
,若![]() 、
、![]() 是
是![]() 两动点,
两动点, ![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时以2cm/s的相同的速度向
两点同时以2cm/s的相同的速度向![]() 、
、![]() 运动。
运动。
(1)四边形![]() 是平行四边形吗?说明你的理由。
是平行四边形吗?说明你的理由。
(2)若![]() cm,
cm, ![]() cm,当运动时间
cm,当运动时间![]() 为多少时,以
为多少时,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为矩形。
为顶点的四边形为矩形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
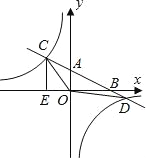
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件.如果降价后商场销售这批衬衫每天盈利1250元,那么衬衫的单价降了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题情境:如图1,在正方形ABCD中,E、F、G、H分别为AB,BC,CD,DA边上的动点,连接EG,HF相交于点O,且∠HOE=∠ADC.试探究:EG与FH的数量关系,并说明理由.

(2)拓展延伸:如图2,在菱形ABCD中,E、F、G、H分别为AB,BC,CD,DA边上的动点,连接EG,HF相交于点O,且∠HOE=∠ADC,试探究:(1)中EG与FH的数量关系还成立吗?并说明理由.
(3)反思提升:若将(2)中的菱形ABCD改为平行四边形ABCD(如图3),AB=a,AD=b,其他条件不变,则![]() 的猜想正确吗?请说明理由.
的猜想正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.
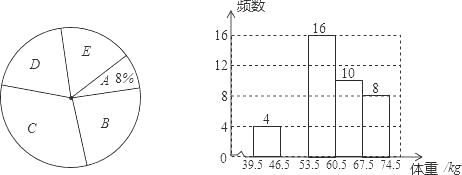
解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com