练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．下列命题中，属于真命题的是（　　）
    A．各边相等的多边形是正多边形B．同角或等角的余角相等
    C．必然事件发生的概率为0D．六边形的内角和等于540°

    分析 根据正多边形定义：各边相等，各内角也相等的多边形是正多边形可得A说法错误；根据余角的性质可得B正确；根据必然事件发生的概率为1可得C错误；根据多边形内角和公式：180°（n-2）可得六边形的内角和等于720°，故D错误．

    解答 解：A、各边相等的多边形是正多边形，说法错误；
    B、同角或等角的余角相等，说法正确；
    C、必然事件发生的概率为0，说法错误；
    D、六边形的内角和等于540°，说法错误；
    故选：B．

    点评 此题主要考查了命题与定理，关键是掌握争正多边形定义、多边形内角和公式、余角的性质、以及必然事件定义．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

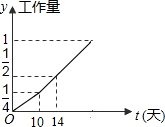    8．甲、乙两个工程队完成某项工程，首先是甲单独做了10天，然后乙队加入合做，完成剩下的全部工程，设工程总量为单位1，工程进度满足如图所示的函数关系，那么实际完成这项工程所用的时间比由甲单独完成这项工程所需时间少（　　）
    A．12天B．14天C．16天D．18天

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．不等式组$\left\{\begin{array}{l}{x+2≤3}\\{\frac{-2x+3}{3}＜3}\end{array}\right.$的解集在数轴上表示为（　　）
    A．B．
    C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

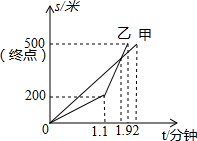    6．在2015年聊城市举办的“划龙舟，庆端午”比赛中，甲、乙两队在比赛时的路程s（米）与时间t（分钟）之间的函数关系图象如图所示，根据图象得到下列结论，其中错误的是（　　）
    A．这次比赛的全程是500米
    B．乙队先到达终点
    C．比赛中两队从出发到1.1分钟时间段，乙队的速度比甲队的速度快
    D．乙与甲相遇时乙的速度是375米/分钟

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

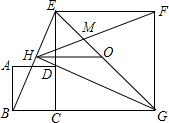    13．如图，正方形ABCD的边与正方形CGFE的边CE重合，O是EG的中点，∠EGC的平分线GH过点D，交BE于点H，连接OH、FH，EG与FH交于点M，对于下面四个结论：①GH⊥BE②HO$\frac{∥}{=}$$\frac{1}{2}$BG；③GH2=GM•GE；④△GBE∽△GMF，其中正确的有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

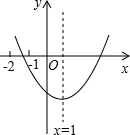    3．如图是二次函数y=ax2+bx+c（a≠0）的图象，有下列判断：①b2＞4ac，②2a+b=0，③3a+c＞0，④4a-2b+c＜0；⑤9a+3b+c＜0．其中正确的是（　　）
    A．①②③B．②③④C．①②⑤D．③④⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图所示，将一副直角三角形拼放在一起得到四边形ABCD，其中∠BAC=45°，∠ACD=30°，点E为CD边上的中点，连接AE，将△ADE沿AE所在直线翻折得到△AD′E，D′E交AC于F点．若AB=3$\sqrt{2}$cm．求：
    （1）试说明BD′平分∠ABC；
    （2）试在线段AC上确定一点P，使得DP+EP的值最小，并求出这个最小值；
    （3）直接写出点D′到BC的距离$\frac{3\sqrt{2}-\sqrt{6}}{2}$cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图1，△ABC为等边三角形，△ADE是△ABC的位似图形，位似比为k：1，点D在AB上，点E在AC上．

    （1）证明：DE∥BC；
    （2）将△ADE绕点A旋转α至△AMN的位置．
    ①如图2，当AM⊥BC时，请你判断AC与MN的位置关系，并说明理由；
    ②若四边形AMCN为菱形，如图3，求旋转角α及k的值；
    ③如图4，当直线MN过点B时，求k与旋转角α（0°＜α＜60°）之间的关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，抛物线y=-$\frac{3}{4}$x2-$\frac{9}{4}$x+3与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，连接AC，BC，把△ABC沿x轴向右平移得到△A′B′C′，AB边上的点O平移到点O′．
    （1）求点B、C的坐标及抛物线的对称轴；
    （2）在平移的过程中，设点B关于直线A′C′的对称点为点F，当点F落在直线AC上时，求△ABC平移的距离；
    （3）在平移过程中，连接CA′，CO′，求△A′CO′周长的最小值．

    查看答案和解析>>

    同步练习册答案